Giáo án Hình học Lớp 7 - Tiết 67 đến 70 - Năm học 2010-2011
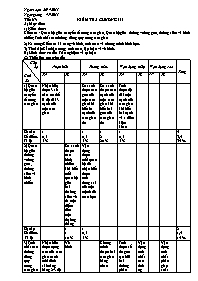
I) Trắc nghiệm: (3 điểm) Chọn câu đúng bằng cách khoanh tròn chữ cái đứng đầu
Câu 1: Phát biểu nào sau là sai
A) Trong một tam giác vuông, cạnh huyền là cạnh lớn nhất.
B) Trong một tam giác, đối diện với cạnh nhỏ nhất là góc nhọn.
C) Trong một tam giác, đối diện với cạnh lớn nhất là góc tù
D) Trong tam giác đều, trọng tâm cách đều ba cạnh.
Câu 2: Tam giác ABC có AB = 4cm, AC = 2cm. Biết độ dài BC là một số nguyên chẵn. Vậy BC bằng
A) 2cm B) 4cm C) 6cm D) 8cm
Câu 3: Bộ 3 độ dài đoạn thẳng có thể là độ dài 3 cạnh của một tam giác là
A) 5cm; 3cm; 2cm B) 4cm; 5cm; 6cm C) 7cm; 4cm; 3cm D) 12cm; 8cm; 4cm
Câu 4: Cho tam giác ABC, AB > AC > BC . Ta có
A) C > B >A
B) B > C > A C) A > B > C
D) A > C> B
Câu 5:Cho G là trọng tâm của tam giác ABC với AM là đường trung tuyến thì
Câu 6:Cho tam giác ABC có A = 800, các đường phân giác BD, CE cắt nhau tại I. Góc BIC có số đo là
A) 800 B) 1000 C) 1200 D) 1300
II) Tự luận: (7 điểm)
Bài 1: Cho tam giác ABC có A = 1000; B = 200.
a) So sánh các cạnh của tam giác ABC. (2 điểm)
b) Vẽ AH vuông góc với BC tại H. So sánh HB và HC. (1 điểm)
Bài 2: Cho tam giác ABC cân tại A có A D là đường phân giác.
a) Chứng minh (2 điểm)
b) Gọi G là trọng tâm của tam giác ABC. Chứng minh ba điểm A; D; G thẳng hàng. (1 điểm)
c) Tính DG biết AB = 13cm ; BC = 10cm (1 điểm)
Ngày soạn: 26/4/2011 Ngày giảng: 4/5/2011 Tiết 67: KIỂM TRA CHƯƠNG III A) Mục tiêu: 1) Kiến thức: Kiểm tra : Quan hệ giữa các yếu tố trong tam giác, Quan hệ giữa đường vuông góc, đường xiên và hình chiếu; Tính chất các đường đồng quy trong tam giác 2) Kí năng:Kiểm tra kĩ năng vẽ hình, tính toán và chứng minh hình học. 3) Thái độ:Cẩn thận trong tính toán, lập luận và vẽ hình. B) Hình thức ra đề: Trắc nghiệm và tự luận C) Thiết lập ma trận đề: Cấp độ Chủ đề Nhận biết Thông hiểu Vận dụng thấp Vận dụng cao Tổng TN TL TN TL TN TL TN TL 1) Quan hệ giữa các yếu tố trong tam giác Nhận biết được 3 số nào có thể là độ dài 3 cạnh của một tam giác So sánh được các góc của một tam giác khi biết ba cạnh của tam giác đó So sánh được các cạnh của một tam giác khi biết hai góc của tam giác đó Tính được độ dài một cạnh của tam giác khi biết hai cạnh và 1 điều kiện khác Số câu Số điểm. Tỉ lệ 1 0,5 5 % 1 0,5 5 % 1 2 20 % 1 0,5 5 % 4 3,5 35 % 2) Quan hệ giữa đường vuông góc , đường xiên và hình chiếu So sánh được các hình chiếu khi biết mối quan hệ giữa hai đường xiên vẽ từ một điểm đến một đường thẳng Vận dụng được mối quan hệ để nhận biết được tính đúng sai của một mệnh đề toán học Số câu Số điểm. Tỉ lệ 1 1 10 % 1 0,5 5 % 2 1,5 15 % 3) Tính chất các đường đồng quy trong tam giác Nhận biết được trọng tam của tam giác cách mỗi đỉnh 1khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó Vẽ hình Chứng minh được hai tam giác bằng nhau Tính được số đo góc tạo bởi hai đường phân giác của tam giác khi biết số đo của góc còn lại Vận dụng tính chất các đường đồng quy để chứng minh ba điểm thẳng hàng Vận dụng tính chất phân giác xuất phát từ đỉnh đối diện với cạnh đáy của tam giác cân để tính độ dài 1 đoạn thẳng Số câu Số điểm. Tỉ lệ 1 0,5 5 % 1 0,5 5 % 1 1,5 15 % 1 0,5 5 % 1 1 10 % 1 1 10 % 5 5 50 % Tổng Số câu Số điểm Tỉ lệ 2 1 10 % 1 1,5 15 % 2 1 10 % 2 3,5 35 % 2 1 10 % 1 1 10 % 1 1 10 % 11 10 100% E) Đề kiểm tra: Trường THCS Đồng Tiến Lớp: 7 Họ, tên: ... . Điểm Lời phê của giáo viên I) Trắc nghiệm: (3 điểm) Chọn câu đúng bằng cách khoanh tròn chữ cái đứng đầu Câu 1: Phát biểu nào sau là sai Trong một tam giác vuông, cạnh huyền là cạnh lớn nhất. Trong một tam giác, đối diện với cạnh nhỏ nhất là góc nhọn. Trong một tam giác, đối diện với cạnh lớn nhất là góc tù Trong tam giác đều, trọng tâm cách đều ba cạnh. Câu 2: Tam giác ABC có AB = 4cm, AC = 2cm. Biết độ dài BC là một số nguyên chẵn. Vậy BC bằng A) 2cm B) 4cm C) 6cm D) 8cm Câu 3: Bộ 3 độ dài đoạn thẳng có thể là độ dài 3 cạnh của một tam giác là A) 5cm; 3cm; 2cm B) 4cm; 5cm; 6cm C) 7cm; 4cm; 3cm D) 12cm; 8cm; 4cm Câu 4: Cho tam giác ABC, AB > AC > BC . Ta có A) C > B >A B) B > C > A C) A > B > C D) A > C> B Câu 5:Cho G là trọng tâm của tam giác ABC với AM là đường trung tuyến thì A) B) C) D) Câu 6:Cho tam giác ABC có A = 800, các đường phân giác BD, CE cắt nhau tại I. Góc BIC có số đo là A) 800 B) 1000 C) 1200 D) 1300 II) Tự luận: (7 điểm) Bài 1: Cho tam giác ABC có A = 1000; B = 200. a) So sánh các cạnh của tam giác ABC. (2 điểm) b) Vẽ AH vuông góc với BC tại H. So sánh HB và HC. (1 điểm) Bài 2: Cho tam giác ABC cân tại A có A D là đường phân giác. a) Chứng minh (2 điểm) b) Gọi G là trọng tâm của tam giác ABC. Chứng minh ba điểm A; D; G thẳng hàng. (1 điểm) c) Tính DG biết AB = 13cm ; BC = 10cm (1 điểm) F) Đáp án và biểu điểm: I)Trắc nghiệm: (0,5.6 = 3 đ) 1C; 2B ; 3B ; 4A ; 5A ; 6D II)Tự luận: Bài Đáp án Điểm 1 a) So sánh các cạnh của ABC. b)So sánh HB và HC. tại H và AB > AC nên HB > HC 1 đ 1đ 1đ 2 Chứng minh Xét có : AD cạnh chung AB = AC vì cân tại A Vậy b)Chứng minh ba điểm A; D; G thẳng hàng. AD là đường trung tuyến mà G là trọng tâm Vậy A; D; G thẳng hàng. c)Tính DG mà vuông tại D có Vậy 0.5 đ 0,5 đ 0,5 đ 0,5 đ 0,25 đ 0,25 đ 0,25 đ 0,25 đ 0,25 đ 0,25 đ 0,25 đ 0,25 đ G) Thống kê điểm: Lớp Số HS 0 -> <3 3 -> <5 5 -> <8 8 -> 10 > = 5 SL % SL % SL % SL % SL % 7A 43 7B 37 ==================================== Ngµy so¹n: 26/4/11 Ngµy gi¶ng: 5/5/2011 TiÕt 68 : «n tËp cuèi n¨m I. Môc tiªu: - KiÕn thøc: - Häc sinh «n tËp hÖ thèng c¸c kiÕn thøc ®É häc vÒ tæng ba gãc cña tam gi¸c, c¸c tr êng hîp b»ng nhau cña hai tam gi¸c. - Kü n¨ng: RÌn kÜ n¨ng vÏ h×nh, ®o ®¹c, tÝnh to¸n, chøng minh, øng dông thùc tÕ. - Th¸i ®é: H×nh thµnh ®øc tÝnh cÈn thËn trong c«ng viÖc, chuyªn cÇn, say mª häc tËp. II. Ph u¬ng tiÖn d¹y häc: - Gi¸o viªn: Gi¸o ¸n, Th íc th¼ng, th íc ®o gãc, com pa ... - Häc sinh: §Ò c ¬ng «n tËp, th íc ®o gãc, com pa, phiÕu häc tËp. III. TiÕn tr×nh bµi d¹y: A. Tæ chøc: SÜ sè: 7A: 7B: B. KiÓm tra Ho¹t ®éng cña gi¸o viªn Ho¹t ®éng cña häc sinh Ho¹t ®éng 1: KiÓm tra bµi cò GV: Em h·y ph¸t biÓu ®Þnh nghÜa tam gi¸c c©n, nªu tÝnh chÊt vÒ gãc cña tam gi¸c c©n. Nªu c¸c c¸ch chøng minh mét tam gi¸c lµ tam gi¸c c©n ? GV: NhËn xÐt vµ cho ®iÓm C. Bµi míi: HS: Ph¸t biÓu ®Þnh nghÜa tam gi¸c c©n, tÝnh chÊt cña nã, c¸c c¸ch chøng minh tam gi¸c lµ tam gi¸c c©n. Ho¹t ®éng 2: ¤n tËp lý thuyÕt C©u 1: GV: Ph¸t biÓu ®Þnh nghÜa tam gi¸c ®Òu, tÝnh chÊt vÒ gãc cña tam gi¸c ®Òu. Nªu c¸c c¸ch chøng minh tam gi¸c lµ tam gi¸c ®Òu ? GV: ChuÈn ho¸ vµ cho ®iÓm. C©u 2: GV: Em h·y ph¸t biÓu ®Þnh lý Pitago (thuËn vµ ®¶o) GV: ChuÈn ho¸ vµ cho ®iÓm. HS: Tr¶ lêi c©u hái 1 Tam gi¸c ®Òu lµ tam gi¸c cã ba c¹nh b»ng nhau. Tam gi¸c ®Òu cã ba gãc b»ng nhau vµ b»ng 600 C¸c c¸ch chøng minh tam gi¸c lµ tam gi¸c ®Òu: C1: Chøng minh tam gi¸c cã ba c¹nh b»ng nhau. C2: Chøng minh tam gi¸c cã ba gãc b»ng nhau. C3: Chøng minh tam gi¸c lµ tam gi¸c c©n vµ cã mät gãc b»ng 600. HS: Ph¸t biÓu ®Þnh lý Pitago. Ho¹t ®éng 3: Lµm bµi tËp luyÖn tËp Bµi tËp 70 SGK GV: Gäi HS ®äc néi dung bµi tËp 70 SGK GV: VÏ h×nh vµ h íng dÉn HS lµm bµi tËp GV: NhËn xÐt vµ ch÷a bµi theo tõng phÇn vµ cho ®iÓm. Bµi tËp 71 SGK GV: Tam gi¸c ABC trong h×nh vÏ 151 SGK lµ tam gi¸c g× ? HS: Ho¹t ®éng nhãm lµm bµi tËp 70 a, c©n à lµ tam gi¸c c©n. b, (c¹nh huyÒn – gãc nhän) à BH = CK c, (c¹nh huyÒn – c¹nh gãc vu«ng) à AH = AK d, à lµ tam gi¸c c©n. HS: Tam gi¸c ABC lµ tam gi¸c vu«ng c©n v×: AB2 = AC2 = 22 + 32 = 13 BC2 = 11 + 52 = 26 = AB2 + AC2 GV: Treo b¶ng phô bµi tËp 67, §iÒn dÊu X vµo « trèng mét c¸ch thÝch hîp. Söa l¹i c¸c c©u sai. GV: Gäi 2 HS lªn b¶ng lµm bµi tËp GV: Gäi HS nhËn xÐt sau ®ã chuÈn ho¸ vµ cho ®iÓm. GV: C¸c tÝnh chÊt cña bµi tËp 68 ® îc suy ra tõ ®Þnh lý nµo ? GV: Yªu cÇu HS lµm theo nhãm sau ®ã ®¹i diÖn lªn b¶ng tr×nh bµy. GV: ChuÈn ho¸ vµ cho ®iÓm c¸c nhãm. GV: Gäi HS ®äc ®Ò bµi GV: VÏ h×nh trªn b¶ng vµ yªu cÇu HS vÏ vµo vë sau ®ã ghi GT vµ KL råi lµm bµi tËp GV: H íng dÉn HS vÏ h×nh b»ng th íc th¼ng vµ com pa GV: Yªu cÇu HS lµm theo nhãm sau ®ã ®¹i diÖn lªn b¶ng tr×nh bµy lêi gi¶i cña nhãm m×nh. GV: Gäi c¸c nhãm nhËn xÐt chÐo GV: ChuÈn ho¸ vµ cho ®iÓm. HS: Lªn b¶ng lµm bµi tËp C©u 1: §óng C©u 2: §óng C©u 3: Sai. VÝ dô tam gi¸c cã ba gãc lµ 700, 600, 500. C©u 4: Sai. Söa l¹i: Trog tam gi¸c vu«ng hai gãc nhän phô nhau. C©u 5: §óng C©u 6: Sai. VÝ dô cã tam gi¸c c©n mµ gãc ë ®Ønh lµ 1000, hai gãc ë ®¸y lµ 400 HS: Ho¹t ®éng nhãm tr¶ lêi c©u hái. HS: Lªn b¶ng lµm bµi tËp C©u a, b ® îc suy ra tõ ®Þnh lý “ Tæng ba gãc cña mét tam gi¸c b»ng 1800 ” C©u c ® îc suy ra tõ ®Þnh lý “ Trong mét tam gi¸c c©n, hai gãc ë ®¸y b»ng nhau ”. C©u d ® îc suy ra tõ ®Þnh lÝ “ NÕu mét tam gi¸c cã hai gãc b»n nhau th× tam gi¸c ®ã lµ tam gi¸c c©n ”. HS: NhËn xÐt chÐo gi÷a c¸c nhãm HS: ®äc néi dung bµi tËp HS: VÏ h×nh vµ lµm bµi tËp TH: D vµ A n»m kh¸c phÝa ®èi víi BC, c¸c TH kh¸c t¬ng tù. Gäi H lµ giao ®iÓm cña AD vµ a. Ta cã: Ta l¹i cã: = 1800 nªn Suy ra V©y AD a D. Cñng cè: GV: Tæng hîp vµ nh¾c l¹i vÒ c¸c ®Þnh nghÜa vµ tÝnh chÊt cña tam gi¸c c©n, tam gi¸c ®Òu. HS: N¾m ® îc c¸c ®Þnh nghÜa vµ tÝnh chÊt cña tam gi¸c c©n, ®Òu. GV: Treo b¶ng phô tam gi¸c vµ mét sè d¹ng tam gi¸c ®Æc biÖt (SGK trang 140). HS: VÏ b¶ng tæng kÕt c¸c tam gi¸c, tam gi¸c ®Æc biÖt E. H íng dÉn vÒ nhµ: - VÒ nhµ tiÕp tôc «n tËp. - ¤n lý thuyÕt vµ bµi tËp ®Ó giê sau «n tËp tiÕp. * Rót kinh nghiÖm sau giê d¹y: ------------------------------------------------ Ngµy so¹n: 26/4/2011 Ngµy gi¶ng: 10/5/2011 TiÕt 69 : «n tËp cuèi n¨m (tt) I. Môc tiªu: - KiÕn thøc: - ¤n tËp kiÕn thøc vÒ ® êng th¼ng vu«ng gãc, ® êng th¼ng song song. Sö dông thµnh th¹o dông cô ®Ó vÏ h×nh. - Kü n¨ng: RÌn kü n¨ng vÏ hai ® êng th¼ng vu«ng gãc, hai ® êng th¼ng song song. BiÕt c¸ch kiÓm tra xem hai ® êng th¼ng cho tr íc cã vu«ng gãc hay song song kh«ng. - Th¸i ®é: H×nh thµnh ®øc tÝnh cÈn thËn trong c«ng viÖc, say mª häc tËp. II. Ph ¬ng tiÖn d¹y häc: - Gi¸o viªn: Th íc th¼ng, b¶ng phô, th íc ®o gãc, ªke... - Häc sinh: §Þnh lÝ, GT vµ KL cña ®Þnh lÝ, c¸ch chøng minh ®Þnh lÝ.. III. TiÕn tr×nh bµi d¹y: A. Tæ chøc: SÜ sè: 7A: 7B: B. KiÓm tra Lång trong bµi häc C. Bµi míi: Ho¹t ®éng 1: ¤n tËp lÝ thuyÕt GV: Treo b¶ng phô h×nh vÏ Mçi h×nh trong b¶ng cho biÕt kiÕn thøc g× ? GV: Gäi 4 HS lªn b¶ng lµm bµi, HS d íi líp lµm theo nhãm (7 nhãm) GV: Gäi c¸c nhãm nhËn xÐt GV: ChuÈn ho¸ HS: Lªn b¶ng lµm bµi HS: NhËn xÐt Nhãm 1 nhËn xÐt nhãm 3 Nhãm 2 nhËn xÐt nhãm 4 Nhãm 3 nhËn xÐt nhãm 1 Nhãm 4 nhËn xÐt nhãm 2 Ho¹t ®éng 2: Bµi tËp luyÖn tËp 1 GV: Treo b¶ng phô H·y tÝnh sè ®o x cña gãc O GV: H íng dÉn: VÏ ® êng th¼ng song song víi a ®i qua ®iÓm O GV: TÝnh gãc O1 vµ gãc O2 GV: Gäi 2 HS lªn b¶ng tÝnh gãc O1 vµ gãc O2 GV: VËy em h·y tÝnh Gãc O = ? GV: Gäi HS nhËn xÐt sau ®ã chuÈn ho¸ vµ cho ®iÓm HS: Quan s¸t h×nh vÏ sau ®ã lªn b¶ng lµm bµi tËp HS: - V× a//c nªn gãc O1 = 380 - V× b//c nªn gãc O2=1800–1320 = 480 HS: x = gãc O = O1+O2 = 860 Ho¹t ®éng 3: Bµi tËp luyÖn tËp 2 GV: T ¬ng tù nh trªn h·y tÝnh sè ®o x trong h×nh 40 GV: Treo b¶ng phô h×nh vÏ 40 SGK GV: Gäi HS lªn b¶ng tÝnh, HS d íi líp lµm vµo vë GV: NhËn xÐt, ®¸nh gi¸ vµ cho ®iÓm. HS: Lªn b¶ng tÝnh x Tõ h×nh vÏ ta cã: a c b c Suy ra a//b Suy ra x + 1150 = 1800 Suy ra x = 1800 – 1150 = 650 Ho¹t ®éng 4: Bµi tËp luyÖn tËp 3 GV: Treo b¶ng phô h×nh vÏ 41 GV: Em h·y tÝnh c¸c gãc E1, G2, G3, D4, A5, B6 ? GV: Yªu cÇu HS lµm theo nhãm vµ lµm vµo phiÕu häc tËp GV: Thu phiÕu vµ treo lªn b¶ng cho c¸c nhãm nhËn xÐt chÐo GV: Treo bµi gi¶i Gãc E1 = 600 Gãc G2 = 1100 Gãc G3 = 700 Gãc D4 = 1100 Gãc A5 = 600 Gãc B6 = 700 HS: Quan s¸t h×nh vÏ vµ lµm vµo phiÕu häc tËp sau dã nép cho GV HS: NhËn xÐt chÐo c¸c nhãm Nhãm 2 nhËn xÐt nhãm 3 Nhãm 3 nhËn xÐt nhãm 4 Nhãm 6 nhËn xÐt nhãm 1 Nhãm 5 nhËn xÐt nhãm 2 D. Cñng cè GV: Em h·y ph¸t biÓu c¸c ®Þnh lÝ ® îc diÔn t¶ b»ng c¸c h×nh vÏ 42 SGK trang 104 HS: Tõ h×nh vÏ ph¸t biÓu ®Þnh nghÜa - Hai ® êng th¼ng cïng vu«ng gãc víi ® êng th¼ng thø ba th× chóng song song víi nhau - Hai ® êng th¼ng cïng song song víi ® êng th¼ng thø ba th× chóng song song víi nhau. GV: NhËn xÐt, ®¸nh gi¸ vµ cho ®iÓm E. H íng dÉn vÒ nhµ: 1. VÒ nhµ «n tËp c¸c c©u hái lÝ thuyÕt ch ¬ng 1. 2. Xem l¹i c¸c d¹ng bµi tËp ®· ch÷a chuÈn bÞ ch÷abµi kiÓm tra häc kú. * Rót kinh nghiÖm sau giê d¹y: ........................................................................................ Ngµy so¹n : 29/4/2011 Ngµy gi¶ng: 16/5/2011 TiÕt 70 : tr¶ bµi thi häc kú ii (phÇn h×nh häc) I. Môc tiªu: - KiÕn thøc: - Häc sinh biÕt ® îc bµi lµm cña m×nh như thÕ nµo vµ ® ưîc ch÷a l¹i bµi KT. - Kü n¨ng: RÌn kü n¨ng tr×nh bµy lêi gi¶i mét bµi to¸n. RÌn th«ng minh, tÝnh s¸ng t¹o - Th¸i ®é: H×nh thµnh ®øc tÝnh cÈn thËn trong c«ng viÖc, say mª häc tËp, GD tÝnh hÖ thèng, khoa häc, chÝnh x¸c. II. Ph ¬ng tiÖn d¹y häc: - Gi¸o viªn: Gi¸o ¸n, chÊm vµ ch÷a bµi kiÓm tra häc k× II ... - Häc sinh: §å dïng häc tËp, phiÕu häc tËp, bót d¹., th íc th¼ng. III. TiÕn tr×nh bµi d¹y: A. Tæ chøc: SÜ sè: 7A: 7B: B. KiÓm tra Lång trong bµi häc C. Bµi míi: GV: Yªu cÇu HS ®äc l¹i ®Ò bµi kiÓm tra häc k× II phÇn h×nh học HS: §äc ®Ò bµi GV cïng HS gi¶i GV nªu ra c¸c lçi thêng gÆp trong khi lµm bµi cña HS D. Rót kinh nghiÖm sau giê d¹y:
Tài liệu đính kèm:
 giao an 7 tiet 6770.doc
giao an 7 tiet 6770.doc





