Giáo án Hình học Khối 8 - Tiết 32: Ôn tập (Chuẩn bị kiểm tra học kỳ I)
I. MỤC TIÊU
- Ôn tập các kiến thức về tứ giác đã học
- Ôn tập các công thức tính diện tích hình chữ nhật, tam giác, hình thang, hình bình hành, hình thoi, tứ giác có hai đường chéo vuông góc.
- Vận dụng các kiến thức trên để giải các bài tập dạng tính toán, chứng minh, nhận biết hình, tìm hiểu điều kiện của hình. thấy được mối quan hệ giữa các hình.
II. CHUẨN BỊ
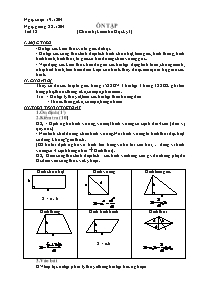
Thầy: sơ đồ các loại tứ giác trang 152 SGV + bài tập 3 trang 32 SGK ghi lên bảng phụ. thước thẳng êke, compa, phấn màu.
Trò: - Ôn tập lý thuyết, làm các bài tập theo hướng dẫn
- Thước thẳng, êke, compa, bảng nhóm
III. TIẾN TRÌNH TIẾT DẠY
1. Ổn định (1’)
2. Kiểm tra (10’)
Bạn đang xem tài liệu "Giáo án Hình học Khối 8 - Tiết 32: Ôn tập (Chuẩn bị kiểm tra học kỳ I)", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Ngày soạn: 19.12.04 Ngày giảng: 22.12.04 ÔN TẬP Tiết 32 (Chuẩn bị kiểm tra Học kỳ I) I. MỤC TIÊU - Ôn tập các kiến thức về tứ giác đã học - Ôn tập các công thức tính diện tích hình chữ nhật, tam giác, hình thang, hình bình hành, hình thoi, tứ giác có hai đường chéo vuông góc. - Vận dụng các kiến thức trên để giải các bài tập dạng tính toán, chứng minh, nhận biết hình, tìm hiểu điều kiện của hình. thấy được mối quan hệ giữa các hình. II. CHUẨN BỊ Thầy: sơ đồ các loại tứ giác trang 152 SGV + bài tập 3 trang 32 SGK ghi lên bảng phụ. thước thẳng êke, compa, phấn màu. Trò: - Ôn tập lý thuyết, làm các bài tập theo hướng dẫn - Thước thẳng, êke, compa, bảng nhóm III. TIẾN TRÌNH TIẾT DẠY 1. Ổn định (1’) 2. Kiểm tra (10’) HS1: - Định nghĩa hình vuông, vẽ một hình vuông có cạnh dài 4cm: (đơn vị quy ước) - Nêu tính chất đường chéo hình vuông. Nói hình vuông là hình thoi đặc biệt có đúng không? giải thích. (HS trả lời định nghĩa vẽ hình lên bảng và trả lời câu hỏi, đúng vì hình vuông có 4 cạnh bằng nhau à Hình thoi). HS2: Điền công thức tính diện tích các hình vào bảng sau: gv đưa bảng phụ để Hs điền vào công thức và ký hiệu. Hình chữ nhật a b a d a h a h a h a d1 d2 h S = a . b Hình vuông Hình tam giác Hình thang Hình bình hành S = a.h Hình thoi 3. Vào bài GV tiếp tục ôn tập phần lý thuyết bằng bài tập trắc nghiệm TL Hoạt động của GV Hoạt động của HS Kiến thức 8’ GV gọi HS trả lời nhanh các câu hỏi: cho biết Đ hay S. 1) Hình thang có hai cạnh bên song song là hình bình hành (Đ) 2) Hình thang c ó 2 cạnh bên bằng nhau là hình thang cân (S) 3) Hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song (Đ) 4) Hình thang cân có một góc vuông là hình chữ nhật (Đ) 5) Tam giác đều là hình có tâm đối xứng 6) Tam giác đều là một đa giác đều (Đ) 7) Hình thoi là một đa giác đều 8) Tứ giác vừa là hình chữ nhật, vừa là hình thoi là hình vuông (Đ) 9) Tứ giác có hai đường chéo vuông góc với nhau và bằng nhau là hình thoi(S) 10)Trong các hình thoi có cùng chu vi thì hình vuông có diện tích lớn nhất.(Đ) 25’ + GV cho HS làm bài tập 35 (SGK) A B C D H O - HS đọc đề bài 1 HS lên bảng. Bài tập: 1) Bài 35 (SGK/129) s Tính diện tích hình thoi có cạnh dài 6cm và một trong các góc của nó có số đo là 600. Giải: Kẻ AH ^ DC DADC có DA = DC và => DADC đều => - GV yêu cầu HS đọc đề, một HS lên bảng vẽ hình. s Nêu cách tính diện tích hình thoi? s gv yêu cẦu 1 HS lên bảng, cả lớp làm vào vở à HS nhận xét. - HS trả lời S = DC . AH - HS lên bảng cách khác: Tương tự tính được B O A D E K C I H + GV cho HS làm bài tập 41 (SGK/132) - GV đưa hình vẽ và đề bài bằng bảng phụ. - Hs quan sát hình vẽ và trả lời câu hỏi và làm bài vào vở. 2. Bài 41 (SGK/132)Giải Ta có: GV a) Hãy nêu cách tính diện tích DDBE? - HS vẽ hình vào vở - HS:. b) b) Nêu cách tính diện tích tứ giác EHIK? + GV đưa đề bài và hình vẽ bằng bảng phụ. - HS: SEHIK = sECH – sKIC = 10,2 – 2,55 = 7,65 (cm)2 3. Bài 161 (SBT/77) B A D E K M G H C - HS có thể nêu cách chứng minh khác. Ví dụ: ED là đường trung bình của DABC và HK là đường trung bình của DGBC. Giải: a) Tứ giác DEHK có: EG = GK = CG DG = GH = BG => Tứ giác DEHK là hình bình hành vì có 2 đường chéo cắt nhau tại trung điểm mỗi đường. a) Chứng minh: Tứ giác DEHK là hình bình hành? - Có nhận xét gì về tứ giác DEHK? Tại sao nói là hình bình hành. b) Tam giác ABC có điều kiện gì thì tứ giác DEHK là hình chữ nhật. A E D C G M B K H => ED // HK // BC và ED =HK=BC => (Kết quả) - HS phát biểu: .. + HS có thể chứng minh cách khác. Ví dụ: Hình bình hành DEHK là hình chữ nhật => ED ^ EH mà ED // BC (cmt) Tương tự EH // AG Nên ED ^ EH => BC ^ AM => DABC cân tại A. b) Hình bình hành DEHK là hình chữ nhật HD = EK BD = CE DABC cân tại A. (Một tam giác cân có hai truyng tuyến bằng nhau). A E D C K H B G (Một tam giác cân => có trung tuyến đồng thời là đường cao) c) Nếu trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình gì? GV đưa hình vẽ sẵn minh họa. - HS trả lời:. Nếu Bd ^ CE thì hình bình hành DEHK là hình thoi vì có hai đường chéo vuông góc với nhau. 4. Dặn dò: (2’) - Ôn tập lý thuyết chương I và II theo hướng dẫn ôn tập, làm lại các dạng bài tập (trắc nghiệm, tính toán, chứng mính, tìm điều kiện của hình). - Chuẩn bị kiểm tra học kỳ I. IV RÚT KN: ....................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................................... TUẦN 20 Ngày soạn 08/01/2008 Ngày giảng 09/01/2008 Tiết 36 §6 DIỆN TÍCH ĐA GIÁC I MỤC TIÊU: Qua bài này HS cần: Nắm chắc phương pháp chung để tính diện tích một đa giác bất kì. Rèn kĩ năng phân tích, chọn phương pháp phân chia đa giác một cách hợp lí để việc tính toán thực hiện được dễ dàng, hợp lí. Biết thực hiện việc vẽ, đo, tính toán một cách chính xác ,cẩn thận. II CHUẨN BỊ: Thầy: Hình vẽ sẵn trên giấy kẻ ô vuông. Phấn màu. Trò : Giấy kẻ ô, thước thẳng có chia khoảng mm, êke, máy tính bỏ túi. III TIẾN TRÌNH TIẾT DẠY: Ổn định: 1’ Kiểm tra: (Không kiểm tra). Vào bài: TL Hoạt động của thầy Hoạt động của trò Ghi bảng 12’ - GV Cho một đa giác tuỳ ý, hãy nêu phương pháp có thể dùng để tính diện tích đa giác? Cơ sở của phương pháp? . GV đưa hình vẽ bằng bảng phụ (đa giác ban đầu) A E B C D - HS vẽ đa giác vào vở, suy nghĩ cách tính diện tích của đa giác đó. A E B D C D’ C’ Chia đa giác thành những tam giác, những tứ giác đơn giản tính được diện tích A B F C E D Tính diện tích của đa giác được đưa về tính diện tích của những tam giác, hình thang. (12’) GV: Thực hiện các phép vẽ, đo cần thiết để tính diện tích của đa giác sau: HS: Làm theo nhóm học tập.(GV phát phiếu học tập) Lớp 8:.. Nhóm: .. Các thành viên: 1/ 2/ 3/ 4/ 5/ 6/ 7/ 8/ 9/ -GV Yêu cầu các nhóm trình bày bài làm của nhóm. -Các nhóm nhận xét. GV nhận xét . Kết luận. TL Hoạt động của thầy Hoạt động của trò Ghi bảng 12’ Luyện tập: GV: Cho HS làm bài tập 38/130 SGK Dữ kiện của bài toán được ghi trên hình vẽ. Hãy tính diện tích của phần con đường EBGF và phần diện tích còn lại của đám đất. -HS sinh hoạt nhóm. Bài làm ghi trên bảng nhóm: SEBGF= FG.CB =50.120 =6000 (m2) SABCD=150.120=18000(m2) S(còn lại)=18000-6000 =2000(m2) A 150 E B 120 D F 50 G C GV: Hãy thực hiện phép đo ( chính xác đến mm). Tính diện tích hình ABCDE (Hình152 SGK) Làm từng HS, phần đo , tính toán, ghi trên phiếu học tập, GV thu và chấm một số HS. - HS: Đo độ dài các đoạn thẳng AC, BG, AH, HK, KC, HE, KD. . Tính diện tích các hình: SABC , SAHE, SHKDE, SKDC. .Tính tổng diện tích các hình trên. B A H K C G E D (Hình 152 SGK) 6’ Củng cố: Nếu diện tích của phần đã tính ở trên là hình của đám đất đã vẽ vớI tỉ lệ xích . Tìm diện tích thực của đám đất đó? HS: - Độ dài thực của các đoạn thẳng đã đo:.. -Tính diện tích các hình : SABC , SAHE, SHKDE, SKDC.trong thực tế. - Tổng diện tích của các hình trên. Dặn dò: 2' -Xem lạI bài , làm bài tập: 39,40 SGK/130 -Chú ý có thể mắc sai lầm khi lấy tổng diện tích của các hình nhân vớI mẫu của tỉ lệ xích để tìm diện tích của hình trong thực tế! -Chuẩn bị ôn tập chương II câu hỏi A và bài tập B trang 131-132 SGK. TRƯỜNG THCS TÂY SƠN Ngày tháng 01 năm 2005 Lớp : 8A/... KIỂM TRA: 1TIẾT Họ và tên:............................... HÌNH HỌC 8 (Chương II) Điểm: Lời phê: Đề: Câu 1: (2đ) Khoanh tròn chữ cái đứng trước kết quả đúng: Tổng số đo các góc của một bát giác là: A. 1080 B. 10800 C. 5400 D. 1350 Một hình thoi có cạnh bằng 6 dm và có góc nhọn bằng 300. Diện tích của hình thoi đó là: A. 18 dm2 B. 72 dm2 C. 36 dm2 D. 9 dm2 Câu 2:(2đ) Chọn câu trả lời đúng: Tính diện tích thực của một hồ nước có sơ đồ là phần gạch sọc trên hình (cạnh của mỗi ô vuông là 1 cm, tỉ lệ ) là: A. 2200 m2 B. 220 m2 C. 2200000 m2 D. 22 m2 Câu 3:(2đ) Tính diện tích tam giác vuông, biết độ dài cạnh huyền 15cm và độ dài một cạnh góc vuông là 12cm. Câu 4:(4đ) Cho hình chữ nhật ABCD có độ dài AB = 90cm và BC = 40cm. Trên các cạnh AB và CD lấy các điểm M và N sao cho AM = CN. Tìm vị trí của M và N, biết rằng diện tích của tứ giác AMCN bằng diện tích hình chữ nhật ABCD. BÀI LÀM: Ngày soạn 16/01/05 Tiết 24 KIỂM TRA 1 TIẾT I. MỤC TIÊU : Kiểm tra kiến thức đã học ở chương II về đa giác lồi, đa giác đều. Kiểm tra các công thức tính diện tích hình thang, hình bình hành, hình thoi, hình chữ nhật, hình tam giác. - Kiểm tra việc vận dụng những kiến thức trên và kĩ năng tính toán, tìm phương pháp để phân chia một hình thành những hình có thể đo đạt, tính toán diện tích. II ĐỀ BÀI : Câu 1: (2đ) Khoanh tròn chữ cái đứng trước kết quả đúng: a)Tổng số đo các góc của một đa giác 9 cạnh là: A. 10800 B. 12600 C. 5400 D. 9000 Hình thoi ABCD có Â = 600, AB = 1 . Diện tích của hình thoi ABCD là: A. B. C. 2 D. 4 Câu 2:(2đ) Chọn câu trả lời đúng: Tính diện tích thực của một hồ nước có sơ đồ là phần gạch sọc trên hình (cạnh của mỗi ô vuông là 1 cm, tỉ lệ ) là: A. 2200 m2 B. 220 m2 C. 2200000 m2 D. 22 m2 Câu 3:(2đ) Tính độ dài cạnh hình thoi. Biết hai đường chéo của hình thoi đó có độ dài là: 12cm, 16cm. Câu 4:(4đ) Cho hình chữ nhật ABCD có độ dài AB = 70cm và BC = 40cm. Trên các cạnh AB và CD lấy các điểm M và N sao cho AM = CN. Tìm vị trí của M và N, biết rằng diện tích của tứ giác AMCN bằng diện tích hình chữ nhật ABCD. III Đáp án, biểu điểm: Câu1: a) Chọn B. (1đ) Chọn B. (1đ) Câu2: Chọn A. (2đ) Câu3: Độ dài cạnh hình thoi là 10cm (2đ) Câu4: SABCD = 2800 cm2 , SAMCN = 560 cm2 (2đ) NC = AM = 14cm , trả lời: (2đ) IV. THỐNG KÊ : Lớp Điểm 9 - 10 7 - 8 5 - 6 3 - 4 1 - 2 Sỉ số sl tl sl tl sl tl sl tl sl tl 8A/5 45 8A/8 51 IV RUT KN: .. Số đo mỗi góc của một ngũ giác đều là: A. 1200 B. 600 C. 1080 D. 540 TRƯỜNG THCS QUANG TRUNG Ngày tháng 01 năm 2005 Lớp : 8A/8. KIỂM TRA: 1TIẾT Họ và tên:............................. HÌNH HỌC 8 (Chương II) Điểm: Lời phê: Đề: Câu 1: (2đ) Khoanh tròn chữ cái đứng trước kết quả đúng: a)Tổng số đo các góc của một đa giác 9 cạnh là: A. 10800 B. 12600 C. 5400 D. 9000 Hình thoi ABCD có Â = 600, AB = 1 . Diện tích của hình thoi ABCD là: A. B. C. 2 D. 4 Câu 2:(2đ) Chọn câu trả lời đúng: Tính diện tích thực của một hồ nước có sơ đồ là phần gạch sọc trên hình (cạnh của mỗi ô vuông là 1 cm, tỉ lệ ) là: A. 2200 m2 B. 220 m2 C. 2200000 m2 D. 22 m2 Câu 3:(2đ) Tính độ dài cạnh hình thoi. Biết hai đường chéo của hình thoi đó có độ dài là: 12cm, 16cm. Câu 4:(4đ) Cho hình chữ nhật ABCD có độ dài AB = 70cm và BC = 40cm. Trên các cạnh AB và CD lấy các điểm M và N sao cho AM = CN. Tìm vị trí của M và N, biết rằng diện tích của tứ giác AMCN bằng diện tích hình chữ nhật ABCD. BÀI LÀM: Ngày soạn 16/01/05 Tiết 35 ÔN TẬP CHƯƠNG II I MỤC TIÊU: HS cần: Hệ thống hoá kiến thức đã học ở chương II về đa giác lồi, đa giác đều. Nắm được các công thức tính diện tích hình thang, hình bình hành, hình thoi, hình chữ nhật, hình tam giác. Vận dụng được những kiến thức trên để rèn luyện kĩ năng tính toán, tìm phương pháp để phân chia một hình thành những hình có thể đo đạt, tính toán diện tích. Rèn luyện tư duy logic, thao tác tổng hợp. II CHUẨN BỊ: GV: Bảng phụ (hình vẽ) và phiếu học ỵâp. HS: Trả lời các câu hỏi và bài tập trong phần ôn tập. III TIẾN TRÌNH TIẾT DẠY: Ổn định: 1’ Kiểm tra: ( Trong khi ôn tập ) Vào bài: TL Hoạt động của thầy Hoạt động của trò Ghi bảng 25’ GV: Treo bảnh phụ hình ảnh bên kèm với hệ thống câu hỏi: .Những hình vẽ trên, những hình nào là đa giác lồi? Vì sao? .Phát biểu định nghĩa đa giác lồi? HS: Quan sát, trả lời và nêu lí do vì sao ABCD, EFGHI, không phải là đa giác lồi. HS: Phát biểu định nghĩa: F B G E A I C D J K O L N M Chú ý: Các đa giác ABCD, EFGHI, không phải là đa giác lồi. GV: Phát phiếu học tập cho HS, điền vào chỗ trống để được câu đúng. Sau khoảng 3 phút GV đề nghị HS trả kời câu cần điền. GV cho nhận xét , sửa sai. HS:Điền vào chỗ trống: Biết tổng số đo các góc của một đa giác có n cạnh là: + ++ = (n-2).1800 Vậy nếu n = 7 thì .. .Đa giác đều là đa giác có . .Biết số đo mỗi góc trong một đa giác đều có n cạnh là: Nếu một ngũ giác đều thì mỗi góc ... Nếu một lục giác đều thì mỗi góc cố số đo là: Viết công thức tính diện tíchmỗi hình sau đây: S= S= S= S= h S= a a h S = b Cho HS điền công thức tính diện tích vào những hình tương ứng.(GV treo bảng phụ đã vẽ các hình) HS Trả lời những công thức tính diện tích mà GV yêu cầu. a a h d2 h d1 S = S = 17’ GV cho HS hoạt động theo nhóm: a) Bài tập 46 SGK/133: Tóm tắt: Cho tam giác ABC, MA=MC, NB=NC. Chứng minh: SABNM = SABC b) Bài tập 42 SGK/132 Cho biết AC//BF. Hãy tìm trong hình vẽ tam giác có diện tích bằng diện tích tứ giác ABCD Từ bài toán trên, suy ra phương pháp vẽ thêm một đoạn thẳng có một đầu là một đỉnh của tứ giác, đầu kia nằm trên một cạnh của tứ giác sao cho chia tứ giác đó thành hai phần có diện tích bằng nhau (AB < CD) HS làm việc theo nhóm, mỗi nhóm hai bàn, làm trên bảng phụ. .SABM = SBMC = SBMN = SMNC = SABM + SBMN = HS: làm việc theo nhóm, mỗi nhóm hai bàn, làm trên bảng phụ. .. A D F C M B SADM = SAFM = SABCD: 2 C + Bài tập 46: M N A B Vẽ hai trung tuyến AN và BM của tam giác ABC. Ta có: SABM = SBMC =SABC SBMN = SMNC = SABC Vậy SABM + SBMN = SABC = SABC Tóm tắt lời giải: a) SABC = SAFC ( chung đáy AC có chiều cao là chiều cao hình thang ABFC) Suy ra SADF = SADC+ SABC = SABCD b) Gọi M là trung điểm của DF, AM chia tứ giácABCD thành hai phần có cùng diện tích. Dặn dò: 2’ Ôn tập theo hướng dẫn, chuẩn bị kiểm tra chương II. Bài tập 43,44,45 SGK/133. IV RUT KN:
Tài liệu đính kèm:
 giao_an_dai_so_khoi_8_tiet_32_on_tap_chuan_bi_kiem_tra_hoc_k.doc
giao_an_dai_so_khoi_8_tiet_32_on_tap_chuan_bi_kiem_tra_hoc_k.doc





