Giáo án Hình học Khối 8 - Tiết 25: Ôn tập chương I - Nguyễn Văn Tú

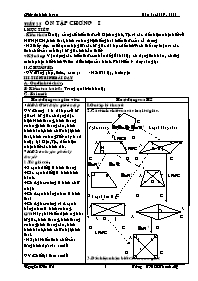
Tiết 25 ôn tập chương i
I. Mục tiêu:
- Kiến thức: Ôn tập củng cố kiến thức về Định nghĩa, T/c và các dấu hiệu nhận biết về HBH, HCN, hình thoi, hình vuông.Hệ thống hoá kiến thức của cả chương
- HS thấy được mối quan hệ giữa các tứ giác đã học dễ nhớ & có thể suy luận ra các tính chất của mỗi loại tứ giác khi cần thiết 
+ Kỹ năng: Vận dụng các kiến thức cơ bản để giải bài tập có dạng tính toán, chứng minh, nhận biết hình & tìm điều kiện của hình. Phát tiển tư duy sáng tạo
II. CHUẩN Bị: 
- GV: Bảng phụ, thước, com pa - HS: Bài tập, ôn luyện
Iii- Tiến trình bài dạy
A- Ôn định tổ chức:
B- Kiểm tra bài cũ: Trong quá trình ôn tập
C- Bài mới:
Hoạt động của giáo viên 
Hoạt động của HS 
* HĐ1: Giới thiệu giờ ôn tập
GV: Chương I ta đã học về tứ giác và tứ giác có dạng đặc biệt: Hình thang, hình thang vuông, hình thang cân, hình bình hành, hình chữ nhật, hình thoi, hình vuông. Tiết này ta sẽ ôn tập lại Đ/n, T/c, dấu hiệu nhận biết các hình đó.
* HĐ2: ôn luyện phần lý thuyết
1. Tứ giác có: 
+ 2 cạnh đối // là hình thang
+ Các cạnh đối // là hình bình hành.
+ Có 4 góc vuông là hình chữ nhật.
+ Có 4 cạnh bằng nhau là hình thoi
+ Có 4 góc vuông và 4 cạnh bằng nhau là hình vuông.
GV: Hãy phát biểu định nghĩa: tứ giác, hình thang, hình thang vuông, hình thang cân, hình bình hành, hình chữ nhật, hình thoi.
- HS phát biểu tính chất của từng hình dựa vào sơ đồ
GV: Chốt lại theo sơ đồ
- GV: Hỏi Khi nào thì ta có 1 tứ giác là hình thang?
- Khi nào thì ta có hình thang là?
+ Hình thang cân
+ Hình thang vuông
+ Hình bình hành
- Khi nào ta có tứ giác là hình bình hành? ( 5 trường hợp)
- Khi nào ta có HBH là:
+ Hình chữ nhật
+ Hình thoi
- Khi nào ta có HCN là hình vuông?
Khi nào ta có hình thoi là hình vuông ?
- Để EFGH là HCN cần có thêm đk gì ?
- HS đọc đề bài & vẽ hình , ghi gt , kl
 B
 / 
 E D M
 / 
 A C 
- GV: Để cm AEBM là hình thoi có thể cm: 4 cạnh của nó bằng nhau:
+ AEBM là hình vuông khi có = 900
muốn vậy AM phải vừa là trung tuyến vừa là đường cao ABC phải là vuông cân.
I.Ôn tập lý thuyết
 / \
 \ 
 / \\
 \\ o /
 _ _
 = O = 
2. Các tính chất của các loại tứ giác.
 B
 C 
 3 góc vuông +++=3600 4 cạnh bằng nhau
 A 
 AB//CD D
 A B A B
 H AB//BC /
 C D D C 
 =900 =
A B =900 A B AB=BC
D 2 cạnh bên // C D C 
 / \
 \ O /
 A B B 
 A C
 D C =900 D 
 AB=BC
 A B 
 / 
 D C
3.Dấu hiệu nhận biết các loại tứ giác
II. Bài tập áp dụng
1.Chữa bài 88/SGK
 B
 E F
A C 
 H G
 D 
 ABCD; E, F, G, H là
GT trung điểm của AB, BC, 
 CD, DA
KL Tìm đk của AC & BD để 
 EFGH là
 a) HCN
 b) Hình thoi
 c) Hình vuông
Chứng minh:
Ta có: E, F, G, H theo thứ tự là trung điểm của AB, BC, CD & DA ( gt) nên:
EF // AC & EF = EF // GH
GH // AC & GH = 	EF = GH
 Vậy EFGH là hình bình hành
a) Hình chữ nhật:
EFGH là HCN khi có 1 góc vuông hay EF//EH
Mà EFEH
Vậy khi ACBD thì EFGH là HCN
b) EFGH là hình thoi khi EF = EH mà ta biết EF ; EH = do đó khi AC = BD thì EF = EH
Vậy khi AC = BD thì EFGH là hình thoi
c)- EFGH là hình vuông khi EFEH & EF = EH theo a & b ta có AC BD thì EFEH 
 AC = BD thì EF = EH
Vậy khi AC BD & AC = BD thì EFGH là hình vuông
2. Chữa bài 89/ SGK
 ABC có = 900
 GT D là trung điểm AB
 M là trung điểm BC
 E đx M qua D
 a) E đx M qua AB
 KL b) AEMC, AEMB là hình gì? Vì sao?
 c) Tính chu vi AEBM khi BC = 4cm
 d) ĐK ABC để AEBM là hình vuông
Chứng minh: 
a) D, M thứ tự là trung điểm của AB, AC nên ta có : DM // AC
AC AB ( gt) mà DM // AC suy ra DM AB (1)
E đx với M qua D do đó ED = DM (2)
Vậy từ (1) & (2) AB là trung điểm của đoạn thẳng EM hay E đx qua AB.
b) AB & EM vuông góc với nhau tại trung điểm của mỗi đường nên AEBM là hình thoi 
 AE //BM hay AE //MC ta lại có EM // AC ( cmt)
Vậy AEMC là HBH
c) AM = AE = EB = BM = = 2 cm
 Chu vi EBMA = 4.2 = 8 cm
EBMA là hình vuông khi AB = EM 
mà EM = AC vậy AEBM là hình vuông khi AB = AC hay ABC là vuông cân
D- Luyên tập - Củng cố:
- Trả lời bt 90/112
+ Hình 110 có 2 trục đx & 1 tâm đx
+ Hình 111 có 2 trục đx & 1 tâm đx.
E- BT - Hướng dẫn về nhà:
- Làm bài 87 ( SGK)
- Ôn lại toàn bộ chương
- Xem trước chương II:
 Đa giác – Diện tích đa giác 
1