Giáo án Hình học 8 - Tiết 47: Luyện tập - Năm học 2009-2010 - Phạm Xuân Diệu

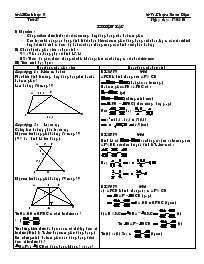
?2
?1
?2
A
B
3
D
C
x
y
4,5
?1
 Tiết 47 Ngày dạy: 17/03/10	Luyện tập
I) Mục tiêu : 
Củng cố kến thức lí thuyế về các trường hợp đồng dạng của hai tam giác 
Rèn luyện kỉ năng vận dụng định lí để nhận biết các tam giác đồng dạng với nhau, lập ra các tỉ số thích hợp để từ đó tính ra được độ dài các đoạn thẳng trong các hình vẽ ở phần bài tập 
II) Chuẩn bị của giáo viên và học sinh : 
 GV : Giáo án, bảng phụ vẽ hình 43, 45
 HS : Thước đo góc, thước thẳng có chia khoảng; làm các bài tập ra về nhà ở tiết trước
III) Tiến trình dạy học : 
Hoạt động của giáo viên
Hoạt động của học sinh
A
B
C
D
O
K
H
A
x
D
C
B
28,5
12,5
A
y
D
x
E
C
B
3
2
6
3,5
Hoạt động 1 : Kiểm tra bài cũ 
Phát biểu định lí trường hợp đồng dạng thứ ba của hai tam giác ?
Làm bài tập 36 trang 79
Hoạt động 2 : Luyện tập 
Cả lớp làm bài tập phần luyện tập 
Một em lên bảng giải bài tập 38 trang 79
( GV đưa hình 45 lên bảng )
Một em lên bảng giải bài tập 39 trang 79
Từ OA.OD = OB.OC ta có tỉ lệ thức nào ?
* ()
Từ những kiến thức đã học nào ta có thể lập được tỉ lệ thức ( Định lý Ta-lét hoặc tam giác đồng dạng )
Em chứng minh hai tam giác nào đồng dạng để có được tỉ lệ thức đó ? 
OAB và OCD có đồng dạng không ? vì sao?
A
B
C
D
E
15cm
20cm
8cm
6cm
Một em lên bảng giải bài tập 40 trang 80
C
BT36 / 79 Giải 
ABCD là hình thang nên AB // CD 
 ( hai góc so le trong )
Hai tam giác ABD và BDC có :
 (gt)
 ( chứng minh trên)
ABD ~ BDC ( theo trường hợp g - g)
Nên hay 
 x2 = 12,5 . 28,5 = 356,25
x = 18,9 (cm) 
BT38 / 79 Giải
Hình 45 có và chúng ở vị trí so le trong nên AB // DE nên theo hệ quả định lí Ta-lét ta có :
Hay x = 
 y = 
BT39 / 79 Giải 
a) ABCD là hình thang suy ra AB // CD 
	OAB ~OCD ( g. g)
	OA.OD = OB.OC (đpcm)
b) AH // KCOHA~OKC (1)
 Từ OAB ~OCD (2)
Từ (1) và (2) Suy ra (đpcm)
BT40 / 80 Giải 
Hai tam giác ADE và ACB có 
Vậy 
Và có góc A chung nên ADE ~ ACB (c.g. c)
Một em lên bảng giải bài tập 42 trang 80
\
Một em lên bảng giải bài tập 43 trang 80
Một em lên bảng giải bài tập 44 trang 80
A
M
D
C
B
N
24
28
Một em lên bảng giải bài tập 45 trang 80
A
B
8
10
D
E
F
6
C
BT42 / 80 Giải 
Các trường hợp đồng dạng Các trường hợp bằng nhau
a)(c.c.c) a) A’B’ = AB; B’C’ = BC
 và A’C’ = AC (c.c.c)
b),(c.g.c) b) A’B’ = AB; B’C’ = BC
 và ( c. g. c)
c) và( g. g ) c) và
 và A’B’ = AB (g. c. g)
BT43 / 80 Giải 
a) Trong hình vẽ đã cho có ba cặp tam giác đồng dạng:
AD // BF ( ABCD là hình bình hành )
EAD ~EBF (1)
EB // DC ( ABCD là hình bình hành )
EBF ~DCF (2)
Từ (1) và (2) suy ra EAD ~DCF 
b) E ở giữa AB suy ra EB = AB - AE = 12 - 8 = 4 (cm)
Từ EAD ~EBF 
Suy ra hay EF = = 5 (cm)
Và hay BF = = ,5(cm)
BT44 / 80 Giải 
a) Hai tam giác ABM và ACN có:
( gt )
= 900
Do đó ABM ~ACN
Vậy 
b) Từ ABM ~ACN
	 (1)
Hai tam giác BMD và CND có :
 ( hai góc đối đỉnh )
	BMD ~CND
	 (2)
Từ (1) và (2) suy ra 
BT45 / 80 Giải 
Hai tam giác ABC và DEF có 
 (gt)
Từ đó ta có :
(cm)
(cm)