Giáo án Đại số Lớp 9 học kì II - Năm học 2011-2012

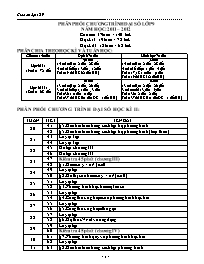
 PHÂN PHỐI CHƯƠNG TRÌNH ĐẠI SỐ LỚP 9
NĂM HỌC: 2011 – 2012
Cả năm: 37 tuần = 140 tiết.
Học kì I: 19 tuần = 72 tiết.
Học kì II: 18 tuần = 68 tiết.
PHÂN CHIA THEO HỌC KÌ VÀ TUẦN HỌC:
Cả năm 140 tiết
Đại số 70 tiết
Hình học 70 tiết
Học kì I:
19 tuần = 72 tiết
40 tiết
14 tuần đầu x 2 tiết = 28 tiết
4 tuần kế tiếp x 3 tiết = 12 tiết 
Tuần 19 thi HKI (2 tiết HH)
32 tiết
14 tuần đầu x 2 tiết = 28 tiết
4 tuần kế tiếp x 1 tiết = 4 tiết
Tuần 17, 18 x 0 tiết = 0 tiết
Tuần 19 thi HKI (2 tiết HH)
Học kì II:
18 tuần = 68 tiết
30 tiết
13 tuần đầu x 2 tiết = 26 tiết
3 tuần kế tiếp x 1 tiết = 3 tiết
Tuần 36 x 0 tiết = 0 tiết
Tuần 37 thi HKII (1 tiết ĐS + 1 tiết HH)
38 tiết
13 tuần đầu x 2 tiết = 26 tiết
3 tuần cuối x 3 tiết = 9 tiết
Tuần 36 x 2 tiết = 2 tiết
Tuần 37 thi HKII (1 tiết ĐS + 1 tiết HH)
PHÂN PHỐI CHƯƠNG TRÌNH ĐẠI SỐ HỌC KÌ II:
TUẦN
TIẾT
TÊN BÀI
20
41
§5. Giải bài toán bằng cách lập hệ phương trình
42
§5. Giải bài toán bằng cách lập hệ phương trình (tiếp theo)
21
43
Luyện Tập
44
Luyện Tập
22
45
Ôn tập chương III
46
Ôn tập chương III
23
47
Kiểm tra 45 phút (chương III)
48
§1. Hàm số y = ax2 (a0
24
49
Luyện tập
50
§2. Đồ thị của hàm số y = ax2 (a0)
25
51
Luyện tập
52
§3. Phương trình bậc hai một ẩn số
26
53
Luyện tập
54
§4. Công thức nghiệm của phương trình bậc hai
27
55
Luyện tập
56
§5. Công thức nghiệm thu gọn
28
57
Luyện tập
58
§6. Hệ thức Vi-ét và ứng dụng
29
59
Luyện tập
60
Kiểm tra 45 phút (chương IV)
30
61
§7. Phương trình quy về phương trình bậc hai
62
Luyện tập
31
63
§8. Giải bài toán bằng cách lập phương trình
64
Luyện tập
32
65
Ôn tập chương IV
66
Ôn tập chương IV
33
67
Ôn tập cuối năm
34
68
Ôn tập cuối năm
35
69
Ôn tập cuối năm
36
37
70
Kiểm tra học kì II
Tuaàn: 20 - Tieát: 41 
Ngày soạn: 19/12/2011
§5: GIẢI BÀI TOÁN BẰNG CÁCH LẬP HỆ PHƯƠNG TRÌNH
Mục tiêu:
1/ Về kiến thức:
Biết cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn. 
2/ Về kĩ năng: 
Bước đầu có kỹ năng giải các loại toán cơ bản được đề cập đến trong SGK.
 3/ Về thái độ
Thấy được ứng dụng của toán học trong đời sống. Linh hoạt sáng tạo khi giải toán.
Chuẩn bị: 
Giáo viên: SGK, SGV, SBT Toán 9.
Học sinh: SGK, SBT Toán 9. Ôn tập lại các bước giải bài toán bằng cách lập phương trình bậc nhất một ẩn số.
Các hoạt động trên lớp:
Ổn định: Kiểm tra sĩ số, tác phong, học cụ.
Kiểm tra bài cũ: Gọi 1 HS đứng tại chỗ nêu các bước giải bài toán bằng cách lập phương trình.
Bài mới:
Yeâu caàu HS traû lôøi ?1
Ñöa caùch giaûi leân maøn hình(baûng phuï, phim trong)
Trong thöïc teá, ñoâi khi chuùng ta khoâng chæ giaûi caùc baøi toaùn baèng caùch laäp phöông trình nhö lôùp 8. Maø coù nhöõng baøi toaùn caàn phaûi ñöa ñeán moät heä phöông trình. Ñoù chính laø noäi dung baøi hoïc hoâm nay.
Hoạt động của thầy
Hoạt động của học sinh
Ghi bảng
Hoạt động 1
 Ñeå giaûi baøi toaùn baèng caùch laäp heä phöông trình, chuùng ta cuõng tieán haønh töông töï .
Cuï theå laàn löôït xeùt caùc ví duï sau:
Giôùi thieäu ví duï 1.
Höôùng daãn HS phaân tích ñeà baøi.
Trong baøi toaùn treân ta thaáy coù hai ñaïi löôïng chöa bieát laø chöõ soá haøng chuïc vaø chöõ soá haøng ñôn vò cuûa soá caàn tìm.
Theo GT khi vieát hai chöõ soá aáy theo thöù töï ngöôïc laïi, ta vaãn ñöôïc moät soá coù hai chöõ soá. Ñieàu ñoù chöùng toû raèng caû hai chöõ soá ñoù ñeàu phaûi khaùc 0.
Khi ñoù ta seõ laàn löôït goïi . . .
?Theo GT1: Hai laàn chöõ soá haøng ñôn vò lôùn hôn chöõ soá haøng chuïc 1 ñôn vò ,khi ñoù ta laäp ñöôïc phöông trình naøo?
?Töø GT2: ta laäp ñöôïc phöông trình naøo?
Löu yù: Trong heä ghi soá thaäp phaân thì soá coù hai chöõ soá x,y ñöôïc vieát döôùi daïng: 10x + y; vieát theo thöù töï ngöôïc laïi seõ laø: 10y + x
?Töø (1),(2) ta ñöôïc heä phöông tình naøo?
Giaûi heä phöông trình vöøa nhaän?
2 HS ñoïc ñeà baøi toaùn.
Nghe GV höôùng daãn vaø suy nghó traû lôøi.
Khi baøi vaøo vôû.
Caù nhaân ñöùng taïi choã traû lôøi cho GV ghi baûng.
Nghe GV höôùng daãn vaø traû lôøi.
1caù nhaân ñöùng taïi choã neâu heä phöông trình.
1HS khaùc leân baûng giaûi.
Ví duï 1: (SGK)
Giaûi:
Goïi chöõ soá haøng chuïc laø x, chöõ soá haøng ñôn vò laø y (x,y>0)
Theo ñeà baøi ta coù : 
2y – x = 1 (1)
(10x+y)-(10y+x)=27
9x-9y=27 x-y=3 (2)
(thoõa maõn ÑK)
Vaäy soá caàn tìm laø: 74
Hoạt động 2
Giải ví dụ 2.
Hướng dẫn HS phân tích đề toán, gọi hai ẩn số rồi lập hệ phương trình.
Yêu cầu HS làm ?3 .
Yêu cầu HS làm ?4 .
Yêu cầu HS làm ?5 .
Phân tích đề toán, gọi ẩn.
Làm ?3 .
Làm ?4 .
Làm ?5 .
Ví dụ 2 SGK tr.21.
Củng cố: 
	Nhấn mạnh các bước giải bài toán bằng cách lập hệ phương trình bậc nhất hai ẩn.
	Nhấn mạnh công thức khi giải các bài toán về chuyển động đều, từ đó suy ra công thức tính v hoặc t khi biết hai đại lượng còn lại.
	Giải bài 28 tr.22 SGK.
	HS làm việc từng đôi để giải và kiểm tra kết quả của nhau. GV gọi một HS lên bảng làm.
Hướng dẫn bài tập về nhà: Làm bài 29, 30 tr.22 SGK.
Tuaàn: 20 - Tieát: 42
Ngày soạn: 19/12/2011
§6. GIẢI BÀI TOÁN BẰNG CÁCH LẬP HỆ PHƯƠNG TRÌNH (tiếp)
A. Mục tiêu:
1/ Về kiến thức:
Biết cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn. Bước đầu có kỹ năng giải các loại toán cơ bản được đề cập đến trong SGK.
2/ Về kĩ năng: 
Bước đầu có kỹ năng giải các loại toán cơ bản được đề cập đến trong SGK 
 3/ Về thái độ:
Thấy được ứng dụng của toán học trong đời sống. Linh hoạt sáng tạo khi giải toán.
Chuẩn bị: 
Giáo viên: SGK, SGV, SBT Toán 9.
Học sinh: SGK, SBT Toán 9. Ôn tập lại các bước giải bài toán bằng cách lập phương trình bậc nhất một ẩn số.
Các hoạt động trên lớp:
1.Ổn định: Kiểm tra sĩ số, tác phong, học cụ.
2.Kiểm tra bài cũ: Gọi 1 HS đứng tại chỗ nêu các bước giải bài toán bằng cách lập hệ phương trình.
3.Bài mới:
Hoạt động của thầy
Hoạt động của học sinh
Ghi bảng
Hoạt động 1
Giải ví dụ 3 tr.22 SGK.
Đây là bài toán thuộc loại gì? (toán năng suất).
Công thức chung để áp dụng cho toán năng suất là gì?
(, từ đó suy ra công thức tính một đại lượng theo hai đại lượng còn lại).
Hướng dẫn HS gọi ẩn, từ đó lập được hệ phương trình.
Yêu cầu HS làm ?6 .
Nếu dạng của bài toán.
Nêu công thức để giải bài toán năng suất.
Gọi ẩn số. Lập hệ phương trình cho bài toán.
Làm ?6 .
Ví dụ 3 (SGK).
Lời giải ví dụ 3 tr.22 SGK.
Hoạt động 2
Yêu cầu HS làm ?7 .
Hướng dẫn HS cách giải.
Gọi ẩn như SGK.
Mỗi ngày hai đội làm được bao nhiêu phần công việc? (Tính theo hai cách, suy ra phương trình).
Từ điều kiện mỗi ngày phần việc đội A làm gấp rưỡi phần việc đội B suy ra phương trình nào?
Giải hệ điều kiện đó tìm x, y.
Rút ra nhận xét: với cách giải này ta được hệ phương trình đơn giản hơn.
Chú ý thêm: các bài toán về hai vòi nước cùng chảy vào một bể cũng coi thuộc loại toán năng suất, do đó vẫn sử dụng công thức cho loại toán năng suất.
Gọi ẩn như SGK.
HS tiến hành giải từng bước dưới sự hướng dẫn của GV.
Tóm tắt lời giải ví dụ 3 theo cách 2.
Gọi ẩn như SGK.
Mỗi ngày hai đội làm được (số phần công việc). Mặt khác do hai đội hoàn thành công việc (cv) trong 24 ngày nên mỗi ngày hai đội làm được (cv), do đó:
	(1)
Vì mỗi ngày phần việc đội A làm gấp rưỡi phần việc đội B nên:
 	(2)
Giải hệ gồm hai phương trình (1), (2), tìm được:
Từ đó kết luận.
4.Củng cố: 
	Nhấn mạnh: Thông thường ta chọn ẩn trực tiếp (thường đề bài hỏi về những đại lượng nào thì đặt luôn các đại lượng đó làm ẩn phụ) thì ta dễ dàng lập hệ phương trình. Tuy nhiên có thể linh hoạt hơn trong việc chọn ẩn để đưa về hệ phương trình dễ giải hơn.
5.Hướng dẫn bài tập về nhà: Giải bài 31, 33, 35, 37 tr.24 SGK. 
Tuaàn: 21 - Tieát: 43
Ngày soạn: 26/12/2011
LUYEÄN TAÄP
Mục tiêu:
1/ Về kiến thức:
 Vận dụng thành thạo cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn.
2/ Về kĩ năng: 
 Linh hoạt khi giải toán, thấy rõ ứng dụng của toán học khi giải các bài toán thực tiễn.
 3/ Về thái độ
 + Rèn luyện tính cẩn thận khi tính toán
Chuẩn bị: 
Giáo viên: SGK, SGV, SBT Toán 9.
Học sinh: SGK, SBT Toán 9.
Các hoạt động trên lớp:
Ổn định: Kiểm tra sĩ số, tác phong, học cụ.
Kiểm tra bài cũ: Gọi một HS lên bảng:
- Nêu các bước giải bài toán bằng cách lập hệ phương trình.
- Giải bài tập 31 tr.23 SGK.
Bài mới:
Hoạt động của thầy
Hoạt động của học sinh
Ghi bảng
Hoạt động 1
Giải bài tập 33 tr.23 SGK.
- Gọi HS nêu cách chọn ẩn và lập hệ phương trình.
- Gọi một HS lên bảng giải hệ phương trình đó và trả lời.
- Một HS đứng tại chỗ nêu cách chọn ẩn.
- Gọi từng HS thiết lập từng phương trình theo các điều kiện của bài toán.
- Một HS lên bảng giải hệ phương trình đó và trả lời.
Bài tập 33 (SGK).
Lời giải bài tập 33 tr.23 SGK.
Hoạt động 2
Giải bài tập 37 tr.23 SGK.
Hướng dẫn HS thảo luận để phân tích bài toán.
Gọi ẩn như thế nào ?
Điều kiện: nếu chuyển động cùng chiều thì cứ 20 giây chúng ta lại gặp nhau thì quãng đường của vật đi nhanh đi được trong 20 giây hơn quãng đường mà vật đi chậm đi trong 20 giây là bao nhiêu ?
(1 vòng, tức là 2π).
Viết phương trình thể hiện mối quan hệ đó.
Tương tự, hướng dẫn HS viết phương trình thể hiện nếu chuyển động ngược chiều thì cứ 4 giây chúng lại gặp nhau.
Giải hệ phương trình tìm được.
Đặt ẩn.
Thảo luận để diễn tả điều kiện: nếu chúng chuyển động cùng chiều thì cứ 20 giây chúng lại gặp nhau.
Viết phương trình thể hiện mối quan hệ đó.
Thảo luận để diễn tả điều kiện: nếu chuyển động ngược chiều thì cứ 4 giây chúng lại gặp nhau.
Viết phương trình thể hiện mối quan hệ đó.
Giải hệ phương trình, đối chiếu với điều kiện để trả lời.
Bài tập 37 (SGK).
Lời giải bài tập 37 tr.23 (SGK).
Hoạt động 3
Giải bài tập 34 tr.23 SGK.
Hướng dẫn HS chia thành các nhóm, thảo luận để tìm ra lời giải.
Yêu cầu các nhóm ghi lời giải vào giấy trong để chiếu lời giải lên bảng. (hoặc ghi lời giải vào vở, sau đó cử một đại diện của nhóm có lời giải xong trước lên bảng trình bày).
Yêu cầu cả lớp thảo luận và bổ sung lời giải của các nhóm.
Chia thành các nhóm, thảo luận để tìm ra lời giải.
Các nhóm ghi lời giải vào giấy trong để chiếu lời giải lên bảng.
Cả lớp thảo luận và bổ sung lời giải của các nhóm.
Bài tập 34 (SGK).
Lời giải bài tập 34 tr.23 SGK.
Củng cố: 
	HS nhắc lại các bước giải bài toán bằng cách lập hệ phương trình. Các công thức chủ yếu với bài toán chuyển động đều và bài toán năng suất.
Hướng dẫn bài tập về nhà: 
	Làm bài tập 36, 38, 39 tr.24 SGK.
Tuaàn: 21 - Tieát: 44
LUYEÄN TAÄP
Ngày soạn: 26/12/2011
A. Mục tiêu:
1/ Về kiến thức:
Vận dụng thành thạo cách giải bài toán bằng cách lập hệ hai phương trình bậc nhất hai ẩn.
2/ Về kĩ năng: 
Linh hoạt khi giải toán, thấy rõ ứng dụng của toán học khi giải các bài toán thực tiễn.
 3/ Về thái độ
+ Có ý thức vận dụng những điều đã học vào giải toán.
B. Chuẩn bị:  ... 
- Ghi nhớ Tóm tắt các kiến thức cần nhớ.
- Tiết sau ôn tập chương IV. Nhớ mang Máy tính bỏ túi.
ÔN TẬP CHƯƠNG IV
Tuaàn: 32 - Tieát: 65,66
Ngaøy soaïn: 12/03/2012
A.Muïc tieâu: 
 	Sau khi hoïc xong baøi naøy, hoïc sinh coù khaû naêng
1. Veà kieán thöùc: 
- Trình bày một cách hệ thống lí thuyết của chương IV:
+ Tính chất và dạng đồ thị của hàm số y = ax2 (a ¹ 0).
+ Các công thức nghiệm cảu phương trình bậc hai.
+ Hệ thức Vi – ét và vận dụng để tính nhẩm nghiệm phương trình bậc hai. Tìm hai số biết tổng và tích của chúng.
+ Giải được phương trình bậc hai bằng đồ thị (qua bài tập 54, 55 – sgk). 
2. Về kỹ năng: Rèn luyện kĩ năng giải pt bậc hai, trùng phương, pt chứa ẩn ở mẫu, phương trình tích..
3. Veà thaùi ñoä: Có ý thức vận dụng kiến thức đã học vào giải bài tập.
B. Chuaån bò : 
- GV: Giaùo aùn, SGK
- HS: Xem tröôùc baøi + SGK
C, Caùc hoaït ñoäng treân lôùp:
1. OÅn ñònh: kieåm tra só soá, taùc phong, duïng cuï hoïc taäp.
2. Kieåm tra baøi cuõ: 
3. Tieán haønh:
Noäi dung baøi daïy
Hoaït ñoäng cuûa thầy
Hoaït ñoäng cuûa hoïc sinh
Hoaït ñoäng 1
* Baøi taäp 54 / SGK. 
2) Ñoái vôùi phöông trình ax2 + bx + c = 0 (a ≠ 0). Vieát coâng thöùc tính r, r’ vaø 3 böôùc laäp luaän tìm nghieäm cuûa phöông trình.
3) Vieát heä thöùc Viet vaø neâu hai tröôøng hôïp ñaëc bieät tính nhaåm nghieäm cuûa phöông trình baäc hai.
4) Neâu caùch tìm hai soá khi bieát toång vaø tích cuûa chuùng.
5) Neâu caùch giaûi phöông trình truøng phöông?
+ GV laàn löôït ñöa ra caùc caâu hoûi oân taäp trong SGK vaø goïi töøng HS ñöùng taïi choã traû lôøi.
+ Daën doø HS xem kyõ baûng toùm taét kieán thöùc trang 61, 62 / SGK.
+ HS traû lôøi caâu hoûi thöù nhaát trong SGK/ phaàn oân taäp chöông IV.
Hoaït ñoäng 2
a) r = b2 – 4ac = (-1)2 – 4.1.(-2) = 9 > 0
Vaäy, phöông trình treân coù hai nghieäm phaân bieät laø:
x1 = 2 ; x2 = – 1
b)
c) Phöông trình hoaønh ñoä giao ñieåm cuûa hai phöông trình treân laø: x2 = x + 2 x2 – x – 2 = 0
Roõ raøng x1 = 2 ; x2 = – 1 laø hoaønh ñoä giao ñieåm cuûa hai ñoà thò treân.
+ GV goïi 3 HS leân baûng laøm cuøng luùc.
+ Ñ/v caâu c, GV höôùng daãn HS laäp phöông trình hoaønh ñoä giao ñieåm. Ñôn giaûn seõ ñöôïc pt ôû caâu a.
* Baøi taäp 55 / SGK 
+ 3 HS leân baûng laøm cuøng luùc. Caùc HS coøn laïi theo doûi vaø söûa sai neáu coù.
Hoaït ñoäng 3
a) 3x4 – 12x2 + 9 = 0
Ñaët t = x2. phöông trình ñaõ cho trôû thaønh:
3t2 – 12t + 9 = 0 t2 – 4t + 3 = 0 (1)
Ta coù a + b + c = 1 – 4 + 3 = 0 
 Vaäy, pt (1) coù hai nghieäm phan bieät laø: 
t2 = 1 ; t2 = 3
Suy ra x1 = 1 ; x2 = – 1 ; x3 = ; x4 = 
b) Giaûi töông töï, ta ñöôïc:
c) Phöông trình voâ nghieäm.
+ Caùch giaûi pt truøng phöông ntn?
+ GV nhaéc nhôû HS: Tröôùc tieân ta nhaåm nghieäm. Neáu khoâng rôøi vaøo 2 tröôøng hôïp ñaëc bieät thì môùi choïn caùch giaûi pt baèng caùch laäp r hay r’.
+ Phaûi tìm caùch bieán ñoåi phöông trình ñaõ cho veà daïng phöông trình coù caùc heä soá a, b, c ñôn giaûn nhaát.
* Baøi taäp 56 / SGK 
+ 3 HS leân baûng laøm cuøng luùc. Caùc HS coøn laïi theo doûi vaø söûa sai neáu coù.
Hoaït ñoäng 4
a) r’ = (m – 1)2 + 7m2 > 0 vôùi moïi giaù trò cuûa m. Do ñoù, phöông trình coù nghieäm vôùi moïi giaù trò cuûa m.
b) Goïi x1 , x2 laø hai nghieäm cuûa phöông trình, ta coù: 
x12 + x22 = (x1 + x2)2 – 2x1.x2 =
 = = 
+ GV höôùng daãn HS caùch laøm.
* Baøi taäp 62 / SGK 
4. Cuûng coá: 
5. Daën doø: 
+ Học bài.ð Xem laïi thaät kyõ caùc kieán thöùc ñaõ oân taäp trong chöông IV.
ð Taäp laøm laïi caùc baøi taâïp ñaõ giaûi vaø laøm tieáp caùc baøi taäp töông töï trong SGK.
ð OÂn taäp thaät kyõ chuaån bò kieåm tra chaát löôïng thi HKII.
Tuaàn: 33 + 34 + 35
Tieát: 67 + 68 + 69
Ngaøy soaïn: 19/03/2012
ÔN TẬP CUỐI NĂM
A.Muïc tieâu: 
 	Sau khi hoïc xong baøi naøy, hoïc sinh coù khaû naêng
1. Veà kieán thöùc: 
Nhắc lại các kiến thức về:
- Căn bậc hai.
- Hàm số bậc nhất, hàm số bậc hai.
- Các bài tập giải toán bằng cách lập phương trình (gồm cả giải bài toán bằn cách lập hệ phương trình).
2. Về kỹ năng:
- Rèn luyện kĩ năng về rút gọn, biến đổi biểu thức, tính giá trị biểu thức và một vài dạng câu hỏi nâng cao trên cơ sở rút gọn biểu thức chứa căn.
- Rèn luyện thêm về kĩ năng giải pt, giải hệ pt, áp dụng hệ thức Vi – ét vào việc giải bài tập.
- Khi giải bài toán bằng cách lập phương trình: phân loại được bài toán, phân tích được các đại lượng và trình bày được bài giải. 
3. Veà thaùi ñoä:
- Có ý thức tự học, tự tin và vượt khó trong học tập.
- Thấy rõ tính thực tế của toán học.
B. Chuaån bò: 
- GV: Giaùo aùn, SGK
- HS: Xem tröôùc baøi + SGK
C, Caùc hoaït ñoäng treân lôùp:
1. OÅn ñònh: kieåm tra só soá, taùc phong, duïng cuï hoïc taäp.
2. Kieåm tra baøi cuõ: 
3. Tieán haønh:
Noäi dung baøi daïy
Hoaït ñoäng cuûa thầy
Hoaït ñoäng cuûa hoïc sinh
Hoaït ñoäng 1
TIEÁT 1:
OÂn Lyù thuyeát:
Baøi taäp:
Baøi 1: Tính caên baäc hai cuûa : 25 , 64 , 16, 121 , 225
 Baøi 2 : Tìm caên baäc hai soá hoïc cuûa 25, 16, 36, 49, 121, 1225
Baøi 3 : Haõy ñieàn chöõ Ñ (ñuùng) hoaëc S (sai) sau cho thích hôïp.
a) 
b) 
c) 
 d) 
e) 
 Baøi 4: Tính :
 a) b) 
 c) d) 
Baøi 5: Ruùt goïn caùc bieåu thöùc sau:
A = 
 Baøi 6: Chöùng toû giaù trò cuûa bieåu thöùc A = laø moät soá nguyeân
+ Goïi HS traû lôøi caùc caâu hoûi:
1) Phaân bieät caên baäc hai vaø caên baäc hai soá hoïc cuûa moät soá thöïc khoâng aâm x. ® Pheùp toaùn tìm caên baäc hai soá hoïc goïi laø pheùp khai phöông.
2) Haèng ñaúng thöùc 
3) Lieân heä giöõa pheùp nhaân vaø pheùp khai phöông.
4) Lieân heä giöõa pheùp chia vaø pheùp khai phöông.
5) Ñöa moät soá ra ngoaøi daáu caên, ñöa thöøa soá vaøo trong daáu caên.
6) Truïc caên thöùc ôû maãu.
7) Khöû maãu cuûa bieåu thöùc laáy caên.
+ GV ghi caùc baøi taäp cho HS thöïc hieän
+ HS traû lôøi
Hoaït ñoäng 2
TIEÁT 2:
OÂn Lyù thuyeát:
Baøi Taäp
Caâu 1: Ñoà thò cuûa hsoá y = (m2 – 1)x ñi qua goùc toaï ñoä O(0 ; 0) khi :
A. m > 1	 B. m < 1	
C. m = 1	 D. m tuyø yù (m R)
Caâu 2: 
Xaùc định a ñeå h số y = (a – 1)x + 3 nghịch biến treân R.
+ HS trình baøy baøi giaûi nhö sau :
Hsoá ñaõ cho nghòch bieán treân R 
Û a – 1 < 0 Û a < 1
Baøi giaûi treân ñuùng hay sai?
A. Ñuùng 	B. Sai
Caâu 3: Haõy xaùc ñònh giaù trò cuûa a ñeå ñoà thò haøm soá y = (2a + 1)x ñi qua ñieåm M(–1 ; 5).
A. a = – 2	B. a = 2
C. a = 3	 D. a = – 3
Caâu 6: Xaùc ñònh m ñeå ñoàng bieán ?
A. m > – 3	 B. m > 0
C. m < 0 	D. m < 3
1. Haøm soá y = f(x) ñoàng bieán (nghòch bieán) treân R khi naøo? 
2) Theá naøo goïi laø haøm soá baäc nhaát ? 
3) Ñoà thò h soá baäc nhaát coù daïng naøo?
4) Haøm soá baäc nhaát ñoàng bieán khi naøo? Nghòch bieán khi naøo?
5) Nhaéc laïi veà hai ñöôøng thaúng song song, caét nhau, truøng nhau?
6) Nhaéc laïi veà heä soá goùc cuûa ñöôøng thaúng vôùi truïc hoaønh.
+ GV treo baûng phuï baøi taäp leân baûng, 
® Gho HS giaûi taïi choã vaøi phuùt. Sau ñoù HS ñöùng taïi choã traû lôøi.
® GV nhaän xeùt
+ HS: Cho x1 , x2 R tuyø yù.
- Neáu x1 < x2 maø f(x1) < f(x2) thì haøm soá y = f(x) ñoàng bieán treân R.
- Neáu x1 f(x2) thì haøm soá y = f(x) nghòch bieán treân R.
2) HS traû lôøi
3) Ñoà thò h/soá y = f(x) laø moät ñöôøng thaúng caét truïc tung taïi ñieåm b vaø caét truïc haønh taïi ñieåm 
4) haøm soá baäc nhaát y = ax + b ñoàng bieán khi a > 0 vaø nghòch bieán khi a < 0.
+ HS traû lôøi 
+ HS giaûi taïi choã vaøi phuùt. Sau ñoù HS ñöùng taïi choã traû lôøi.
Hoaït ñoäng 3
TIEÁT 3:
OÂn Lyù thuyeát:
Baøi Taäp
Caâu 1: Pt naøo sau ñaây voâ nghieäm ?
A. 2x – x2 = 0	 
B. 4 – 3x2 = 0
C. 2x2 – 1 = 0	 
D. 1 + 3x2 = 0
Caâu 2: Tính bieät thöùc cuûa phöông trình 
A. = 11 + 	
B. = 11 – 	
C. = 11 + 
D. = 11
Caâu 3: Vôùi giaù trò naøo cuûa m thì phöông trình x2 – (2m – 1)x + m(m – 2) = 0 coù hai nghieäm phaân bieät ?
A. m > 	 B. m > 
C. m < 	 D. m < 
Caâu 4: Soá nghieäm cuûa phöông trình 
– x2 + 2(m + 1)x + = 0 laø:
A. 0	 B. 1	
C. 2	 D. Tuyø thuoäc vaøo giaù trò cuûa m.
Caâu 5: Bieát phöông trình x2 – (3m + 1)x – 2 = 0 coù hai nghieäm phaân bieät x1, x2. Tính m ñeå x1 + x2 = – 4 ?
A. m = 3	 B. m = – 3
C. m = 	 D. m = 
1) Haõy nhaéc laïi caùch giaûi phöông trình baèng caùch laäp r ?
2) Haõy nhaéc laïi caùch giaûi phöông trình baèng caùch laäp r’ ?
3) Haõy nhaéc laïi heä thöùc Vi-et vaø hai tröông hôïp tính nhaåm nghieäm? 
+ GV treo baûng phuï baøi taäp leân baûng, 
® Gho HS giaûi taïi choã vaøi phuùt. Sau ñoù HS ñöùng taïi choã traû lôøi.
® GV nhaän xeùt
+ HS traû lôøi 
+ HS giaûi taïi choã vaøi phuùt. Sau ñoù HS ñöùng taïi choã traû lôøi.
4. Cuûng coá: Töøng phaàn sau moãi tieát
5. Daën doø: + Học bài.
+ Xem laïi taát caû caùc kieán thöùc ñaõ hoïc töø ñaàu naêm.
+ Xem laïi caùch giaûi phöông trình baèng caùch laäp r , r’; caùc coâng thöùc tính nhaåm nghieäm; baøi toaùn tìm hai soá khi bieát toång vaø tích cuûa chuùng.
+ OÂn taäp thaät kyõ chuaån bò kieåm tra chaát löôïng thi HKII.
Tuaàn: 37 - Tieát: 70
Ngaøy soaïn: 04/04/2012
Bài: KIỂM TRA HỌC KỲ II
(ĐỀ DỰ KIẾN)
______________
I Mục tiêu:
- Kiểm tra khả năng lĩnh hội các kiến thức trong học kỳ II của HS.
- Rèn khả năng tư duy.
- Rèn kĩ năng tính toán, chính xác, hợp lí.
- Biết trình bày rõ ràng, mạch lạc.
II Đề:
I.Trắc nghiệm: (3 điểm)
	Hãy chọn câu trả lời mà em cho là đúng nhất.
Câu 1: Phương trình bậc hai ax2 + bx + c = 0 ( a ≠ 0) có nghiệm khi:
 	A. D 0	C. D = 0 	D. D ³ 0
Câu 2: Tích hai nghiệm của phương trình là:
A. 	B. – 1 	C. 	D. Kết quả khác
Câu 3: Nghiệm của hệ phương trình là:
A.(x = 3; y = 3)	B.(x = –3; y = –3)	 C.(x = 3; y = –3) D. (x = –3; y = 3)
Câu 4: Tính chất biến thiên của hàm số y = là:
A. Đồng biến với mọi giá trị của x	
B. Nghịch biến với mọi giá trị của x	
C. Đồng biến khi x > 0, nghịch biến khi x < 0
D. Đồng biến khi x 0
Câu 5: Diện tích của hình quạt tròn có góc ở tâm 900, bán kính 2cm là:
A. p (cm2)	B. 2p (cm2)	C. (cm2)	D. Kết quả khác
Câu 6: Thể tích của hình trụ có bán kính đáy 1cm, chiều cao gấp đôi bán kính đáy là:
A. 4p (cm3)	B. 2p (cm3)	C. p (cm3)	D. Kết quả khác
II. Tự luận: (7 điểm)
Bài 1: 	Cho hai hàm số y = x2 và y = – 2x + 3.
	a) Vẽ các đồ thị của hai hàm số này trên cùng một hệ trục tọa độ.
	b) Tìm tọa độ giao điểm của hai đồ thị đó.
Bài 2: 	Giải các phương trình sau:
	a) 3x2 – 5x = 0	b) – 2x2 + 8 = 0
	c) 2x2 – 3x – 2 = 0	d) x4 – 4x2 – 5 = 0
Bài 3: Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Ba đương cao AE, BF, CK cắt nhau tại H. Tia AE, BF cắt đường tròn tâm O lần lượt tại I và J.
Chứng minh tứ giác AKHF nội tiếp đường tròn.
Chứng minh hai cung CI và CJ bằng nhau.
Chứng minh hai tam giác AFK và ABC đồng dạng với nhau
Bài 4: Chứng minh trong hai phương trình ax2 + bx + c = 0 và 
ax2 + cx + b – c – a = 0 ít nhất có một phương trình có nghiệm với a ≠ 0.