Đề kiểm tra học kỳ II môn Toán Lớp 8 - Năm học 2010-2011 - Trường THCS Tô Châu

TRƯỜNG TIỂU HỌC TÔ CHÂU
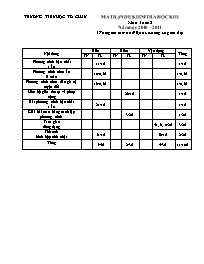
MA TRẬN ĐỀ KIỂM TRA HỌC KÌ II
Môn: Toán 8
Năm học: 2010 – 2011
(Thời gian làm bài 90 phút, không kể giao đề)
Nội dung
Biết
Hiểu
Vận dụng
Tổng
TN
TL
TN
TL
TN
TL
Phương trình bậc nhất
1 ẩn
1a-1đ
1-1đ
Phương trình chứa ẩn
ở mẫu
1c-0,5đ
1-0,5đ
Phương trình chứa dấu giá trị tuyệt đối
1b-0,5đ
1-0,5đ
Liên hệ giữa thứ tự và phép cộng
2b-1đ
1-1đ
Bất phương trình bậc nhất
1 ẩn
2a-1đ
1-1đ
Giải bài toán bằng cách lập phương trình
3-2đ
1-2đ
Tam giác 
đồng dạng
4a, b, c-2đ
3-2đ
Thể tích 
hình hộp chữ nhật
5a-1đ
5b-1đ
2-2đ
Tổng
5-4đ
2-3đ
4-3đ
11-10đ
TRƯỜNG TIỂU HỌC TÔ CHÂU
ĐỀ KIỂM TRA HỌC KÌ II
Môn: Toán 8
Năm học: 2010 – 2011
(Thời gian làm bài 90 phút, không kể giao đề)
Câu 1(2đ): Giải các phương trình
3x – 3 = 15 – 3(x + 4) 
|x – 1| = 2x + 5
Câu 2( 2đ)
Giải bất phương trình sau và biểu diễn tập nghiệm trên trục số
3x – 2(x – 1) > 2x + 4(x – 2)
Cho a > b, chứng minh rằng: a + 5 > b – 2
Câu 3(2đ): Một người đi xe máy từ A đến B với vận tốc 30 km/h. Đến B người đó làm việc trong 1 giờ rồi quay về A với vận tốc 24 km/h. Biết tổng thời gian từ lúc đi đến khi về đến A hết 5 giờ 30 phút. Tính quãng đường AB ?
Câu 4(2đ): Cho tam giác ABC vuông tại A, AB = 24 cm, AC = 32 cm. Kẻ đường cao AH. 
S
	a. Chứng minh DAHC DCAB
S
	b. Chứng minh DAHB DCHA
	c. Tính độ dài các đoạn thẳng BC, AH, CH, BH
Câu 5(2đ): Một bể nước hình hộp chữ nhật có chiều dài là 2m, rộng 1,2m, cao 1m. 
2m
1,2m
1m
a. Tính thể tích của bể
	b. Người ta đổ vào bể 60 thùng nước, mỗi thùng chứa 20 lít nước thì nước trong 
 bể cao bao nhiêu ? 
TRƯỜNG TIỂU HỌC TÔ CHÂU
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KÌ II
Môn: Toán 8
Năm học: 2010 – 2011
(Thời gian làm bài 90 phút, không kể giao đề)
Bài
Đáp án
Điểm
Bài 1
a. 3x – 3 = 15 – 3(x + 4) 3x – 3 = 15 – 3x – 12
 3x + 3x = 15 – 12 + 3
 6x = 6 
 x = 1
 S = {1}
0,5đ
0,5đ
b. Điều kiện: 2x + 5 0 x 
Ta có: |x – 1| = 2x + 5 x – 1 = 2x + 5 hoặc x – 1 = – 2x – 5
* x – 1 = 2x + 5 x = – 6 ( loại)
* x – 1 = – 2x – 5 3x = – 4 x = ( thỏa mãn) 
 Vậy phương trình có 1 nghiệm x = 
0,25đ
0,25
c. Điều kiện: x 2 và x – 2 
Ta có: 
 x + 2 + x – 2 = 1 2x = 1 x = (thỏa mãn)
Vậy S = 
0,25
0,25đ
Bài 2
a. Ta có: 3x – 2(x – 1) > x + 4(x – 2) 3x – 2x + 2 > 2x + 4x – 8
 x + 2 > 6x – 8 
 2+ 8 > 6x – x 
 5x < 10 x < 2
 S = {x R| x < 2}
)
2
0
0,5đ
0,5đ
b. Ta có: a > b => a + 5 > b + 5 (tính chất thứ tự và phép cộng) (1)
 Do 5 > – 2 nên b + 5 > b – 2 (tính chất thứ tự và phép cộng) (2)
 Từ (1) và (2) => a + 5 > b – 2 (tính chất bắc cầu)
0,25đ
0,25đ
0,5đ
Bài 3
Đổi 5h30’ = 5,5 h
Gọi x là độ dài quãng đường AB ( x > 0, km)
Thời gian người đó đi từ A đến B là: (h)
Thời gian người đó đi từ B về A là: (h)
Do người đó ở lại B làm việc 1 giờ, nên ta có phương trình: 
++ 1 = 5,5
 4x + 5x + 120 = 5,5.120
 9x = 540
 x = 60 (thỏa mãn)
Vậy quãng đường AB dài 60 km
0,25đ
0,25đ
0,25đ
0,5đ
0,25đ
0,5đ
Bài 4
A
B
C
H
1
2
24
32
0,5đ
S
a. Chứng minh được: DAHB DCAB 
0,5đ
S
b. Chứng minh được: DAHB DCHA
0,5đ
c. Tính được BC = 40 cm
 Tính được AH = 19,2 cm
 Tính được BH = 14,4 cm
 Tính được CH = 25,6 cm
0,5đ
Bài 5
2m
1,2m
1m
x
a. Thể tích của bể nước là: V = 2.1,2.1 = 2,4 m3
1đ
b. Thể tích nước được đổ vào bể là: 
V = 60.20 = 1200 lít = 1200dm3 = 1,2 m3
Gọi chiều cao mực nước trong bể là x (m), ta có: 
2. 1,2. x = 1,2 x = 0,5 (m)
Vậy mực nước trong bể cao 0,5m hay 50cm. 
0,5đ
0,5đ
 Tô Châu, ngày 02 tháng 04 năm 2011
 Người ra đề 
 Dương Đình Hiển