Đề kiểm tra học kỳ I môn Toán Lớp 8 - Lê Xuân Tam

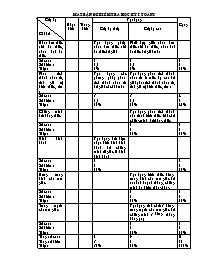
Ma trận đề kiểm tra học kỳ I toán 8
Cấp độ
Chủ đề
Nhận biết
Thông hiểu
Vận dụng
Cộng
Cấp độ thấp
Cấp độ cao
Nhân đơn thức với đa thức, nhân hai đa thức
Vận dụng phép nhân đơn thức với đa thức để giải 
Phối hợp giữa nhân dơn thức với đa thức, nhân hai đa thức để giải toán
Số câu : 
Số điểm :
Tỉ lệ : 
1
0,5
5%
1
0,5
5%
2
1
10%
Phân tích thành nhân tử, tính giá trị biểu thức, tìm x
Vận dụng các phương pháp phân tích thành nhân tử để giải các bài toán
Vận dụng phân tích thành nhân tử ở mức độ cao để giải phân tích thành nhân tử, tính giá trị biểu thức, tìm x
Số câu : 
Số điểm :
Tỉ lệ :
3
1,5
15%
3
2,5
25%
4
2
40%
Chứng minh bất đẳng thức
Vận dụng phân tích thành nhâ tử và kiến thức khác để chứng minh bất đẳng thức
Số câu : 
Số điểm :
Tỉ lệ : 
1
1
10%
1
1
10%
Hình bình hành
Vận dụng đấu hiệu nhận biết hình bình hành để chứng minh tứ giác là hình bình hành
Số câu : 
Số điểm :
Tỉ lệ : 
1
1
10%
1
1
10%
Đương trung bình của tam giác
Vận dụng kiến thức đường trung bình của tam giác để so sánh đoạn 2 thẳng, chứng minh ba điểm thẳng hàng
Số câu : 
Số điểm :
Tỉ lệ : 
2
2
20%
2
2
20%
Trung tuyến của tam giác
Vận dụng tính chất 3 đường trung tuyến của tam giác để chứng minh 3 đường thẳng đồng quy
Số câu : 
Số điểm :
Tỉ lệ : 
1
1
10%
1
1
10%
Tổng số câu : 
Tổng số điểm 
Tỉ lệ :
5
3
30%
8
7
70%
6
10
100%
phòng gd&đt thạch thành
trường thcs thành mỹ
Giáo viên : Lê Xuân Tam
đề kiểm tra học kì I môn toán 8
năm học : 2011 - 2012
Thời gian làm bài : 90 phút
Câu 1 (1đ) Tính : 
 a, b,
Câu 2 ( 2đ) 
 Phân tích các đa thức sau thành nhân tử 
 a, b, 
 c, c, 
Câu 3 (2đ)
 	a, Tính giá trị biểu thức : A = tại x = 3
 	b, Tìm x biết : 
Câu 4 (4đ)
Cho tam giác ABC , M là trung điểm của AC, N là trung điểm của AB. Lấy điểm D đối xứng với N qua M. Gọi O là giao điểm của BD và NC 
a, Chứng minh rằng : BNDC là hình bình hành
b, Chứng minh : 
c, Gọi P là trung điểm của BC . Chứng minh rằng : 3 điểm : M,O,P thẳng hàng
d, Gọi K là trung điểm của AD . Chứng minh rằng : AO, DN, BK đồng quy
Câu 5 (1đ)
Chứng minh rằng : Với mọi x,y,z
Hướng dẫn chấm đề học kì I Toán 8
Câu
Nội dung
Điểm
Câu 1
a, 
b, 
0,5
0,25
0,25
Câu 2 
 a, 
 b, 
 c, 
 c, 
0,5
0,25
0,25
0,25
0,25
0,25
0,25
Câu 3
a, 
Ta có : A = 
 = 
Thay số ta có : A = 
 b, 
0,25
0.25
0,5
0,25
0,25
0,25
0,25
Câu 4
a, (1đ)
b, (1đ)
 c, (1đ)
 d, (1đ)
C
N
M
O
P
D
A
K
B
a, Theo gt ta có MN là đường trung bình của ABC
 MN //= BC (1)
Vì D và N đối xứng nhau qua M 
 ND = 2 MN (2)
Từ (1) và (2) ND //= BC
 BNDC là hình bình hành
b,
 Chứng minh được MO là đường trung bình của ACN
 MO = AN
 Mà AN = AB (gt)
 MO = AB
c, 
Theo câu (b) MO// AB (3)
 Chứng minh được : PO là đương trung bình của BCN
 PO// AB (4)
Từ (3) và (4) ba điểm : M,O, P thẳng hàng
d, 
Theo (gt ) ta có : DN là trung tuyến của ADB (*)
Theo câu (a) suy ra : AO là trung tuyến của ADB (2*)
K là trung điểm của BD nên ta có :
 BK là trung tuyến của ADB (3*)
Từ (*) , (2*) và (3*) ta có : AO, DN, BK đồng quy
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
0,25
Câu 5
Ta có : 
Ta thấy biểu thức trên đúng với mọi x, y,z (đpcm)
0,5
0,5
Chú ý :
Bài hình : học sinh không vẽ hình hoặc vẽ hình không đúng thì không chấm điểm
Học sinh làm cách khác mà dúng vẫn chấm điểm tối đa