Đề kiểm tra chương I môn Hình học Lớp 8 (Có ma trận và đáp án)

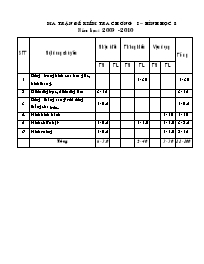
	Ma trận đề kiểm tra chương I – Hình học 8
Năm học: 2009 - 2010 
STT
Nội dung chủ yếu
Nhận biết
Thông hiểu
Vận dụng
Tổng
TN
TL
TN
TL
TN
TL
1
Đường trung bình của tam giác, hình thang.
1-3.0
1-3.0
2
Đối xứng trục, đối xứng tâm
3-1.5
3-1.5
3
Đường thẳng song2 với đường thẳng cho trước.
1- 0.5
1- 0.5
4
Hình bình hành
1-1.0
1-1.0
5
Hình chữ nhật
1- 0.5
1- 1.0
1- 1.0
3- 2.5
6
Hình vuông
1- 0.5
1- 1.0
2-1.5
Tổng
6- 3.0
2-4.0
3-3.0
11-10.0
Đề kiểm tra Chương I
Bài 1 (3điểm): Câu nào đúng, câu nào sai ? 
Khoảng cách giữa hai đường thẳng song2 là khoảng cách từ một điểm tuỳ ý trên đường thẳng này đến đường thẳng kia. 
Hình bình hành có tâm đối xứng là giao điểm hai đường chéo. 
Hình thang cân có trục đối xứng là đường thẳng đi qua trung điểm 2 cạnh đáy. 
Hình chữ nhật có hai đường chéo vuông góc với nhau. 
Hình thoi có hai đường chéo bằng nhau là hình vuông. 
Hình vuông là hình có hai trục đối xứng. 
Bài 2 (3điểm): 
Cho hình thang ABCD(AB//CD). Gọi M, N theo thứ tự là trung điểm của AD, BC. Đường chéo BD cắt MN tại K . Biết AB = 8cm; CD = 12cm . Tính độ dài đoạn thẳng MN, MK, NK.
Bài 3 (4điểm)
 Cho hình bình hành ABCD có AC vuông góc với CB. Gọi M là trung điểm của AB, E là điểm đối xứng với C qua M.
Chứng minh: Tứ giác AEBC là hình chữ nhật.
Cho AB = 6cm; góc ABC = 600. Tính AC?
Từ A kẻ Ax song song với EC cắt BC tại F. Chứng minh: AC, BD, EF đồng quy.
Tìm điều kiện của hình bình hành ABCD để hình chữ nhật AEBC là hình vuông?
	 Người ra đề	 Lãnh đạo duyệt:	
 Nguyễn Đức Hoài	
 Đáp án - biểu điểm
Bài 1: (3điểm)
a.Đ : 0,5 đ	c. Đ : 0,5 đ	e. Đ : 0,5 đ	
b.Đ : 0,5 đ 	d. S : 0,5 đ 	f. S : 0,5 đ
Bài 2: (3điểm)
Vẽ hình đúng : 0,25 đ
C/m MN là đường trung bình của
 hình thang ABCD: 0,5 đ
 Tính MN = = 10 cm: 0,5 đ
C/m được K là trung điểm của BD : 0,5 đ
C/m được MK là đường trung bình của ABD : 0,5 đ
Tính được MK = AB = 4 cm : 0,5 đ
Tính được NK = MN-MK = 6 cm : 0,25 đ
Bài 3: (4điểm)
Vẽ hình đúng ( 0,5 đ )
a/Ta có: AM = MB (gt); EM = MC (E đối xứng với C qua M)
AB ầ EC = {M} ị AEBC là hình bình hành
Mà AC ^ CB (gt) ị ACB = 900ị AEBC là hình chữ nhật 
 ( 0,75 đ )
b/ Xét DACB ta có: AM = MB (gt) 
ị MC = (t/c trung tuyến thuộc cạnh huyền của D vuông)
ị CM = MB ị DMCB vuông cân tại M
Mặt khác: = 600 ị DCMB là tam giác đều ị CB = MB = CB = 3cm (0,5 đ)
Trong DvuôngACB có: AB2 = AC2 + CB2 (ĐL Pytago)
AC2 = AB2 – CB2 ị AC2 = 62 – 32 ị AC2 = 27 ị AC = cm (0,5 đ)
c/ Gọi AC ầ BD = {O} ị AO = OC (t/c hình bình hành)
 Xét tứ giác AECF có: AF // EC (Ax // EC); 
 AE // CF (AE // CB)ị AECF là hình bình hành. (0,5 đ)
Mà O là trung điểm của đường chéo ACị O là trung điểm của đường chéo EF
Hay E, O, F thẳng hàngị AC, BD, EF đồng quy tại O	(0,5 đ)
d/ Giả sử AEBC là hình vuông ị CB = CA (t/c hình vuông) 
 ị DACB là tam giác vuông cân = 450
Vậy khi hình bình hành ABCD có ABC = 450 thì hình chữ nhật AEBC là hình vuông.
	(0,75 đ)