Đề kiểm tra 1 tiết môn Hình học Lớp 8 - Trường THCS Trung Đông (Có ma trận và đáp án)

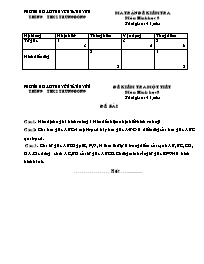
Phòng gd &đt huyện tân uyên
Trường thcs trung đồng
Ma trận đề kiểm tra
Môn: Hình học 8
Thời gian: 45phút
Nội dung
Nhận biết
Thông hiểu
Vận dụng
Tổng điểm
Tứ giác
1
3
3
5
2
8
Hình đố xứng
2
2
1
2
Phòng gd &đt huyện tân uyên
Trường thcs trung đồng
Đề Kiểm tra một tiết
Môn: Hình học 8
Thời gian: 45phút
Đề bài
Câu 1. Nêu định nghĩa hình vuông ? Nêu dấu hiệu nhận biết hình vuông?
Câu 2: Cho tam giác ABC và một trục d hãy tam giác A’B’C’ là đối xứng của tam giác ABC qua trục d.
 Câu 3. Cho tứ giác ABCD gọi E, F, G, H theo thứ tự là trung điểm của cạnh AB, BC, CD, DA. Các đường chéo AC, BD của tứ giác ABCD. Chứng minh rằng tứ giác EFGH là hình bình hành.
..................Hết...................
Đáp án – Biểu điểm
Câu
Hướng dẫn chấm
Biểu điểm
1
Định nghĩa : Hình vuông là tứ giác có 4 góc vuông và bốn cạnh bàng nhau.
Dấu hiệu nhận biết :
Hình chữ nhật có hai cạnh kề bàng nhau là hình vuông
Hình chũ nhật có hai dduwownhf chéo vuông góc với nhau là hình vuông
Hình cũ nhật có một dường chéo là đường phân giác của một góc là hình vuông
Hình thoi có một góc vuông là hình vuông
Hình thoi có hai đường chéo bàng nhau là hình vuông
1
2
2
Vẽ hình chính xác 
2
3
Vẽ đúng hình ghi đúng giả thiết kết luận
- Xét EFGH có :
 EB = EA ; FB = FC (gt) 
 EF là đg Tb của ABC , 
 EF // AC 
 EF = AC (1) 
- Tương tự : HG // AC .
 HG = AC , (2),
 Từ (1) và (2) ta suy ra : 
 EF // HG ( cùng // AC) ,
 EF = HG ( cùng = AC ).
- Nên : EFGH là hbh .
1
4