Chuyên đề Học cách vẽ đường phụ qua việc chứng minh một định lí Hình học Lớp 8 - Lê Trọng Châu
Các bạn biết không ? Định lí “Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy” của lớp 8 có rất nhiều cách chứng minh đấy.
Xin được giới thiệu một số cách chứng minh định lí trên, hi vọng rằng qua đó các bạn cũng như tôi, sẽ tích lũy được nhiều kinh nghiệm dựng hình phụ để giải toán hình học.
Không mất tính tổng quát, ta xét tam giác ABC có phân giác AD (D thuộc BC), ĐABC ≥ ĐACB. Ta cần chứng minh AB/AC = DB/DC (*).
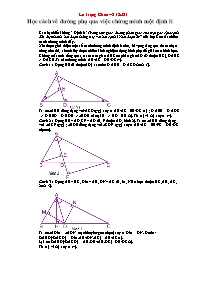
Cách 1 : Dựng BE (E thuộc AD) sao cho Đ ABE = Đ ACD (hình 1).
Ta có ∆ABE đồng dạng với ͧACD (g-g) suy ra AB/AC = EB/DC (1) ; Đ AEB = Đ ADC => Đ BED = Đ BDE => ∆BDE cân tại B => BD = BE (2). Từ (1) và (2) suy ra (*).
Cách 2 : Dựng BE ^ AD, CF ^ AD (E, F thuộc AD, hình 2). Ta có ∆ABE đồng dạng với ∆ACF (g-g) ; ∆BDE đồng dạng với ∆CDF (g-g) suy ra AB/AC = EB/FC = DB/DC (đpcm).
Cách 3 : Dựng AH ^ BC, DM ^ AB, DN ^ AC (H, M, N lần lượt thuộc BC, AB, AC, hình 3).
Học cách vẽ đường phụ qua việc chứng minh một định lí Các bạn biết không ? Định lí “Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn ấy” của lớp 8 có rất nhiều cách chứng minh đấy. Xin được giới thiệu một số cách chứng minh định lí trên, hi vọng rằng qua đó các bạn cũng như tôi, sẽ tích lũy được nhiều kinh nghiệm dựng hình phụ để giải toán hình học. Không mất tính tổng quát, ta xét tam giác ABC có phân giác AD (D thuộc BC), ĐABC ≥ ĐACB. Ta cần chứng minh AB/AC = DB/DC (*). Cách 1 : Dựng BE (E thuộc AD) sao cho Đ ABE = Đ ACD (hình 1). Ta có ∆ABE đồng dạng với ͧACD (g-g) suy ra AB/AC = EB/DC (1) ; Đ AEB = Đ ADC => Đ BED = Đ BDE => ∆BDE cân tại B => BD = BE (2). Từ (1) và (2) suy ra (*). Cách 2 : Dựng BE ^ AD, CF ^ AD (E, F thuộc AD, hình 2). Ta có ∆ABE đồng dạng với ∆ACF (g-g) ; ∆BDE đồng dạng với ∆CDF (g-g) suy ra AB/AC = EB/FC = DB/DC (đpcm). Cách 3 : Dựng AH ^ BC, DM ^ AB, DN ^ AC (H, M, N lần lượt thuộc BC, AB, AC, hình 3). Ta có ∆ADM = ∆ADN (cạch huyền-góc nhọn) suy ra DM = DN. Do đó : S(ABD)/S(ACD) = DM.AB/(DN.AC) = AB/AC (1). Lại có S(ABD)/S(ACD) = AH.DB/(AH.DC) = DB/DC (2). Từ (1) và (2) suy ra (*). Cách 4 : Qua B vẽ đường thẳng song song với AD, cắt đường thẳng AC tại E (hình 4). Xét ∆CBE, AD // BE, ta có DB/DC = AE/AC (1). Cũng vì AD // BE mà AD lại là phân giác của Đ BAC, dễ dàng chứng minh được Đ AEB = Đ ABE => ∆ABE cân tại A => AB = AE (2). Từ (1) và (2) suy ra (*). Cách 5 : Qua D dựng các đường thẳng song song với AB, AC, lần lượt cắt AC, AB tại E, F (hình 5). Ta có ∆BFD đồng dạng với ∆DEC (g-g) suy ra DB/DC = BF/DE = DF/CE = (BF + DF)/(DE + CE). Mặt khác, dễ thấy AEDF là hình thoi nên suy ra DB/DC = AB/AC (đpcm). * Với các cách kẻ hình phụ sau, các bạn hãy thử tiếp tục chứng minh định lí trên bằng những cách khác : Cách 6 (SGK Toán 8, tập 2, trang 66) : Qua B vẽ đường thẳng song song với AC, cắt đường thẳng AD tại E (hình 6). Cách 7 : Qua D dựng đường thẳng song song với AB, qua A dựng đường thẳng song song với BC, hai đường thẳng này cắt nhau tại E. DE cắt AC tại F (hình 7). Cách 8 : Trong ∆ABC, dựng hai đường cao CE và BF, chúng lần lượt cắt AD tại K, H. Đường thẳng qua C song song với AD cắt BF tại I (hình 8). Cách 9 : Dựng qua B đường thẳng vuông góc với AB ; dựng qua C đường thẳng vuông góc với AC, hai đường thẳng này cắt nhau tại K. AD cắt BK, CK lần lượt tại E, F. Dựng qua B đường thẳng song song với AD, cắt CK tại G (hình 9). Cách 10 : Qua B, C dựng các đường thẳng song song với AD, cắt đường thẳng qua D song song với AC lần lượt tại F, E. Đường thẳng qua F song song với AB cắt AD tại M.
Tài liệu đính kèm:
 Hoc cach ve duong phu qua viec chung minh mot dinh li.doc
Hoc cach ve duong phu qua viec chung minh mot dinh li.doc





