Chuyên đề Bồi dưỡng học sinh giỏi môn Vật lí Lớp 8 - Phần I: Phương pháp giải bài tập máy cơ đơn giản - Năm học 2009-2010
* Phương pháp:
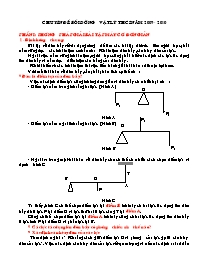
- Do xà có hai điểm tựa (hai giá đỡ) xà chịu tác dụng của ba lực FA, FB và P. Với loại toán này cần phải chọn điểm tựa
- Để tính FA phải coi điểm tựa của xà tại B.
- Để tính FB phải coi điểm tựa của xà tại A.
Áp dụng điều kiện cân bằng của đòn bẩy cho từng trường hợp để giải bài toán.
Với loại toán này cần chú ý: các lực nâng và trọng lực còn thoả mãn điều kiện cân bằng của lực theo phương thẳng đứng có nghĩa P = FA + FB.
Bài giải:
Trọng lượng của xà bằng: P = 10.120 = 1200 (N)
Trọng lượng của xà tập trung tại trọng tâm G của xà.
Xà chịu tác dụng của 3 lực FA, FB, P
Để tính FA ta coi xà là một đòn bẩy có điểm tựa tại B. Để xà đứng yên ta có:
FA.AB = P.GB => (N)
Để tính FB ta coi xà là một đòn bẩy có điểm tựa tại A xà đứng yên khi:
FB.AB = P.GA = > (N)
Vậy lực đỡ của bức tường đầu A là 750 (N), của bức tường đầu B là 450 (N).
ĐS: 750 (N), 450 (N)
Chuyên đề bồi dưỡng vật lý THCS năm 2009 - 2010 Phần I: Phương pháp giải bài tập máy cơ đơn giản 1- Định hướng chung: Bài tập về đòn bẩy rất đa dạng nhưng để làm các bài tập đó trước tiên người học phải nắm vững được các khái niệm cơ bản như: Khái niệm đòn bẩy, cánh tay đòn của lực. Ngoài việc nắm vững khái niệm, người học cũng phải biết xác định các lực tác dụng lên đòn bẩy và nắm được điều kiện cân bằng của đòn bẩy. Khi đã hiểu rõ các khái niệm thì việc tiến hành giải bài toán sẽ thuận lợi hơn. Với mỗi bài toán về đòn bẩy, cần phải phân tích cụ thể như : * Đâu là điểm tựa của đòn bẩy? Việc xác định điểm tựa cũng không đơn giản vì đòn bẩy có nhiều loại như : O F1 F2 - Điểm tựa nằm trong khoảng hai lực (Hình A) O F1 F2 Hình A - Điểm tựa nằm ngoài khoảng hai lực (Hình B) Hình B - Ngoài ra trong một bài toán về đòn bẩy còn có thể có nhiều cách chọn điểm tựa ví dụ như hình CO B A F T Hình C Ta thấy, hình C có thể chọn điểm tựa tại điểm B khi này có hai lực tác dụng lên đòn bẩy đó là lực F tại điểm O và lực thứ hai là lực căng T tại điểm A. Cũng có thể chọn điểm tựa tại điểm A khi này cũng có hai lực tác dụng lên đòn bẩy là lực kéo F tại điểm O và phản lực tại B. * Các lực tác dụng lên đòn bẩy có phương chiều như thế nào? * Xác định cánh tay đòn của các lực Theo định nghĩa : “ Khoảng cách giữa điểm tựa O và phương của lực gọi là cánh tay đòn của lực”. Việc xác định cánh tay đòn của lực rất quan trọng vì nếu xác định sai sẽ dẫn đến kết quả sai. Trên thực tế học sinh rất hay nhầm cánh tay đòn với đoạn thẳng từ điểm tựa đến điểm đặt của lực. Sau khi phân tích có thể áp dụng điều kiện cân bằng của đòn bẩy để giải bài toán. 2. Phân loại bài tập và phương pháp giải bài tập. Bài tập về “Đòn bẩy” có rất nhiều loại cụ thể có thể chia ra làm nhiều loại như sau: Loại 1: Xác định lực và cánh tay đòn của lực Bài toán1: Người ta dùng một xà beng có dạng như hình vẽ để nhổ một cây đinh cắm sâu vào gỗ. a) Khi tác dụng một lực F = 100N vuông góc với OB tại đầu B ta sẽ nhổ được đinh. Tính lực giữ của gỗ vào đinh lúc này ? Cho biết OB bằng 10 lần OA và a = 450. b) Nếu lực tác dụng vào đầu B vuông góc với tấm gỗ thì phải tác dụng một lực có độ lớn bằng bao nhiêu mới nhổ được đinh? FC F F’ A O B H * Phương pháp : Xác định cánh tay đòn của lực F và FC Vì FC vuông góc với OA nên OA là cánh tay đòn của FC a) Vì F vuông góc với OB nên OB là cánh tay đòn của F b) Vì F có phương vuông góc với mặt gỗ nên OH là cánh tay đòn của F’ sau khi đã xác định đúng lực và cánh tay đòn của lực ta áp dụng điều kiện cân bằng của đòn bẩy và tính được các đại lượng cần tìm Lời giải: a) Gọi FC là lực cản của gỗ. Theo quy tắc cân bằng của đòn bẩy ta có: FC . OA = F.OB FC = b) Nếu lực F’ vuông góc với tấm gỗ, lúc này theo quy tắc cân bằng của đòn bẩy ta có: FC.OA = F’.OH Với ( vì DOBH vuông cân) => (N) Đ/S: 1000 N; Bài toán 2: Hai bản kim loại đồng chất tiết diện đều có cùng chiều dài l = 20cm và cùng tiết diện nhưng có trọng lượng riêng khác nhau d1 = 1,25 d2. Hai bản được hàn dính lại ở một đầu O và được treo bằng sợi dây. Để thanh nằm ngang người ta thực hiện hai biện pháp sau: a) Cắt một phần của thanh thứ nhất và đem đặt lên chính giữa của phần còn lại. Tìm chiều dài phần bị cắt. l l O b) Cắt bỏ một phần của bản thứ nhất. Tìm phần bị cắt đi. * Phương pháp: Trong mỗi lần thực hiện các biện pháp cần xác định lực tác dụng và cánh tay đòn của lực. + ở biện pháp 1: Vì cắt một phần của bản thứ nhất và lại đặt lên chính giữa của phần còn lại nên lực tác dụng không thay đổi, cánh tay đòn của lực này thì thay đổi. + ở biện pháp 2: Do cắt bỏ một phẩn của bản thứ nhất nên cả lực và cánh tay đòn của lực đều thay đổi. - Khi xác định được lực và cánh tay đòn của lực ta áp dụng điều kiện cân bằng của đòn bẩy vào giải bài toán: Lời giải: a) Gọi x là chiều dài phần bị cắt. Do đó được đặt lên chính giữa của phần còn lại nên trọng lượng của bản thứ nhất không thay đổi Vì thanh nằm cân bằng nên ta có: O l x Gọi S là tiết diện của mỗi bản, ta có: => d1 (l-x) = d2(l) ú Với d1 = 1,25 d2 l = 20 => Vậy chiều dài phần bị cắt là: 4 cm b) Gọi y là phần bị cắt bỏ đi trọng lượng còn lại của bản là Do thanh cân bằng nên ta có: => => ú => D’ = 400 – 80 = 320 => > 20 cm 20 – 17,89 = 2,11 (cm) Vậy chiều dài phần bị cắt bỏ là 2,11 cm ĐS: 4 cm; 2,11 cm Loại 2: Chọn điểm tựa của đòn bẩy Bài toán 1: Một chiếc xà không đồng chất dài l = 8 m, khối lượng 120 kg được tì hai đầu A, B lên hai bức tường. Trọng tâm của xà cách đầu A một khoảng GA = 3 m. Hãy xác định lực đỡ của tường lên các đầu xà P FB FA B A G * Phương pháp: - Do xà có hai điểm tựa (hai giá đỡ) xà chịu tác dụng của ba lực FA, FB và P. Với loại toán này cần phải chọn điểm tựa - Để tính FA phải coi điểm tựa của xà tại B. - Để tính FB phải coi điểm tựa của xà tại A. áp dụng điều kiện cân bằng của đòn bẩy cho từng trường hợp để giải bài toán. Với loại toán này cần chú ý: các lực nâng và trọng lực còn thoả mãn điều kiện cân bằng của lực theo phương thẳng đứng có nghĩa P = FA + FB. Bài giải: Trọng lượng của xà bằng: P = 10.120 = 1200 (N) Trọng lượng của xà tập trung tại trọng tâm G của xà. Xà chịu tác dụng của 3 lực FA, FB, P Để tính FA ta coi xà là một đòn bẩy có điểm tựa tại B. Để xà đứng yên ta có: FA.AB = P.GB => (N) Để tính FB ta coi xà là một đòn bẩy có điểm tựa tại A xà đứng yên khi: FB.AB = P.GA = > (N) Vậy lực đỡ của bức tường đầu A là 750 (N), của bức tường đầu B là 450 (N). ĐS: 750 (N), 450 (N) Bài toán 2: (áp dụng) P M A B TB TA B’ A’ Một cái sào được treo theo phương nằm ngang bằng hai sợi dây AA’ và BB’. Tại điểm M người ta treo một vật nặng có khối lượng 70 kg. Tính lực căng của các sợi dây AA’ và BB’. Cho biết: AB = 1,4 m; AM = 0,2m. Bài giải: Trọng lượng của vật nặng là: P = 10.70 = 700 (N) Gọi lực căng của các sợi dây AA’ và BB’ lần lượt là: TA và TB. Cái sào chịu tác dụng của 3 lực TA, TB và P. Để tính TA coi sào như một đòn bẩy có điểm tựa tại B. Để sào nằm ngang ta có: TA.AB = P.MB => (N) Để tính TB coi A là điểm tựa. Để sào nằm ngang ta có: TB.AB = P.MA => (N) Vậy: Lực căng của sợi dây AA’ là 600 (N) Lực căng của sợi dây BB’ là 100 (N) ĐS: 600 (N); 100 (N) Loại 3: Khi đòn bẩy chịu tác dụng của nhiều lực * Phương pháp: - Xác định tất cả các lực tác dụng lên đòn bẩy - Xác định các lực làm đòn bẩy quay theo cùng một chiều áp dụng quy tắc sau: “Đòn bẩy sẽ nằm yên hoặc quay đều, nếu tổng tác dụng của các lực làm đòn bẩy quay trái bằng tổng tác dụng của các lực làm đòn bẩy quay phải” Bài toán 1: Một chiếc xà đồng chất tiết diện đều. Khối lượng 20 kg, chiều dài 3 m. Tì hai đầu lên hai bức tường. Một người có khối lượng 75 kg đứng cách đầu xà 2m. Xác định xem mỗi bức tường chịu tác dụng một lực bằng bao nhiêu? Bài giải: P1 FB FA B A O G P Các lực tác dụng lên xà là: - Lực đỡ FA, FB - Trọng lượng của xà P = 10.20 = 200 (N) - Trọng lượng của người P1 = 10.75 = 750 (N) Vì xà đồng chất tiết diện đều nên trọng tâm của xà sẽ ở chính giữa xà => GA = GB = 1,5 m Giả sử người đứng ở O cách A là OA = 2 m Để tính FB coi đầu A là điểm tựa, áp dụng quy tắc cân bằng của đòn bẩy khi có nhiều lực tác dụng ta có: FB.AB = P.AG + P1.AO => (N) FA.AB = P.GB + P1.OB => (N) Vậy mỗi tường chịu tác dụng một lực là 600 (N) với tường A và 350 (N) với tường B ĐS: 600 (N), 350 (N) A O B C C Bài toán 2: Một người muốn cân một vật nhưng trong tay không có cân mà chỉ có một thanh cứng có trọng lượng P = 3N và một quả cân có khối lượng 0,3 kg. Người ấy đặt thanh lên một điểm tựa O trên vật vào đầu A. Khi treo quả cân vào đầu B thì thấy hệ thống cân bằng và thanh nằm ngang. Đo khoảng cách giữa vật và điểm tựa thấy và Hãy xác định khối lượng của vật cần cân. Bài giải Các lực tác dụng lên thanh AC - Trọng lượng P1, P2 của các vật treo tại A và B P2 P P1 I O C B A - Trọng lượng P của thanh tại trung điểm của thanh thanh cân bằng P1 = OA = P.OI + P2.OB => P1 = Với P2 = 10 m P2 = 10.0,3 = 3 (N) (N) Khối lượng của vật là: m = (kg) ĐS: 0,9 kg Loại 4: Lực đẩy Acsimét tác dụng lên vật treo ở đòn bẩy Với dạng toán liên quan đến lực đẩy Acsimét cần nhớ một số công thức hay sử dụng: F = d.V. Trong đó: F là lực đẩy Acsimét D là trọng lượng riêng của chất lỏng V là thể tích chất lỏng bị vật chiếm chỗ Cần nhớ các quy tắc hợp lực + Hợp lực của hai lực F1, F2 cùng phương ngược chiều có độ lớn là: F = | F1- F2 | + Hợp lực của hai lực F1, F2 cùng phương cùng chiều có độ lớn là F = F1 + F2 * Phương pháp giải của dạng toán liên quan đến lực đẩy Acsimet - Khi chưa nhúng vật vào trong chất lỏng, đòn bẩy thăng bằng xác định lực, cánh tay đòn và viết được điều kiện cân bằng của đòn bẩy. - Khi nhúng vào trong một chất lỏng, đòn bẩy mất cân bằng. Cần xác định lại điểm tựa, các lực tác dụng và cánh tay đòn của các lực. Sau đó áp dụng điều kiện cân bằng của đòn bẩy để giải bài toán. Bài toán 1: (áp dụng) Hai quả cầu A, B có trọng lượng bằng nhau nhưng làm bằng hai chất khác nhau, được treo vào đầu của một đòn cứng có trọng lượng không đáng kể FB FA P P O O’ B A là có độ dài l = 84 cm. Lúc đầu đòn cân bằng. Sau đó đem nhúng cả hai quả cầu ngập trong nước. Người ta thấy phải dịch chuyển điểm tựa đi 6 cm về phía B để đòn trở lại thăng bằng. Tính trọng lượng riêng của quả cầu B nếu trọng lượng riêng của quả cầu A là dA = 3.104 N/m3, của nước là dn = 104 N/m3 Bài giải: Vì trọng lượng hai quả cầu cân bằng nhau nên lúc đầu điểm tựa O ở chính giữa đòn: OA = OB = 42 cm Khi nhúng A, B vào nước O'A = 48 cm, O'B = 36 cm Lực đẩy Acsinet tác dụng lên A và B là: Hợp lực tác dụng lên quả cầu A là: P – FA Hợp lực tác dụng lên quả cầu B là: P – FB Để đòn bẩy cân bằng khi A, B được nhúng trong nước ta có: (P – FA). O’A = (P – FB).O’B Hay các giá trị vào ta có: ú ú (N/m3) Vậy trọng lượng riêng của quả cầu B là: dB = 9.104 (N/m3) ĐS: 9.104 (N/m3) Bài toán 2: (áp dụng) Hai quả cầu cân bằng nhôm có cùng khối lượng được treo vào hai đầu A, B của một thanh kim loại mảnh nhẹ. Thanh được giữ thăng bằng nhờ dây mắc tại điểm giữa O của AB. Biết OA = OB = l = 25 cm. Nhúng quả cầu ở đầu B vào nước thanh AB mất thăng bằng. Để thanh thăng bằng trở lại ta phải dời điểm treo O về phía nào? Một đoạn bao nhiêu? Cho khối lượng riêng của nhóm và nước lần lượt là: D1 = 2,7 g/cm3; D2 = 1 g/cm3 Bài giải: Khi quả cầu treo ở B được nhúng vào nước, ngoài trọng lượng P nó còn chịu tác dụng của lực đẩy Acsimet nên lực tổng hợp giảm xuống. Do đó cần phải dịch chuyển điểm treo về phía A một đoạn x để cho cánh tay đòn của quả cầu B tăng lên. ( l +x ) ( l -x ) F P P O B A Vì thanh cân ... ướng thẳng đứng xuống dưới và đặt tại trung điểm O của AB (OA = OB). Theo quy tắc cân bằng ta có: P.OB = T.BH => T= (N) = (N) ĐS: , Bài toán 2: Một khối trụ lục giác đều đặt trên mặt sàn. Một lực tác dụng F theo phương ngang đặt vào đỉnh C như hình vẽ. Trụ có thể quay quanh A. a) Xác định độ lớn của lực F để khối trụ còn cân bằng trọng lượng của khối trụ là P = 30 N b) Lực F theo hướng nào thì độ lớn bé nhất. Tính Fmin (lực F vẫn đạt tại C) F’ F D A B C F E I’ I O P Bài giải: C A B F a) Gọi cạnh chủa khối trụ lục giác là . Khối trụ chịu tác dụng của trọng lượng P và lực F Để khối trụ còn cân bằng ta có: F.AI = P.AH Với (do DOAD đều và AI là đường cao) Từ đó => (N) b) Khi F thay đổi hướng thì AI tăng dần (I đến vị trí I’ trên hình). Do đó lực F giảm dần và AI lớn nhất khi F theo hướng của cạnh CE. Lúc này (hai lần của đường cao tam giác đều) Thật vậy gọi góc ta có AI’ = AF.cos và AI’ lớn nhất khi =0 (cos=1) lúc đó AI’ = AF Để khối trụ còn cân bằng ta có: FMin. AF = P.AH => (N) ĐS: (N), (N) Loại 6: Khi điểm tựa dịch chuyển Xác định giá trị cực đại, cựa tiểu. Bài toán 1: Cho một thước thẳng AB đồng chất tiết diện đều, có độ dài l=24 cm trọng lượng 4N. Đầu A treo một vật có trọng lượng P1 = 2 N. Thước đặt lên một giá đỡ nằm ngang CD = 4 cm. Xác định giá trị lớn nhất và nhỏ nhất của khoảng cách BD để cho thước nằm cân bằng trên giá đỡ l2 l1 O1 O2 E D C P3 P2 P1 B A Bài giải: Xét trạng thái cân bằng của thước quanh trục đi qua mép D của giá đỡ ứng với giá trị nhỏ nhất của AD. Lúc đó thước chia làm hai phần: + Phần BD có trọng lượng P3 đặt ở G1 là trung điểm của DB + Phần OA có trọng lượng P2 đặt ở G2 là trung điểm của AD Mép D ở điểm E trên thước. Điều kiện cân bằng của trục quay D là: P3.AD + P2.GE = P1.G1D ú (1) (với l2 = AD, l1 = ED) Về thước thẳng đồng chất tiết diện đều nên trọng lượng của một phần thước tỷ lệ với chiều dài của phần đó ta có: ; l2 = (l – l1) ; P1 = 2 N = Thay vào (1) ta được ú ú (cm) Giá trị lớn nhất của BD là l1 = 16 cm. Lúc đó điểm D trùng với điểm E trên thước BE = BD = 16 cm Nếu ta di chuyển thước từ phải sang trái sao cho điểm E trên thước còn nămg trên giá CD thì thước vẫn cân bằng cho tới khi E trùng với C thì đến giới hạn cân bằng E lệch ra ngoài CD về phía trái thì thước sẽ quay quanh trục C sang trái. Vậy giá trị nhỏ nhất của BD khi C trùng đến E là BE = BC Mà BC = BD + DC => BD = BC – DC = 16 – 4 = 12 (cm) ĐS: 16 cm, 12 cm Bài toán 2: Một thanh thẳng đồng chất tiết diện đều có trọng lượng P = 100 N, chiều dài AB = 100 cm, được đặt cân bằng trên hai giá đỡ ở A và C. Điểm C cách tâm O của thước một đoạn OC = x a) Tìm công thức tính áp lực của thước lên giá đỡ ở C theo x b) Tìm vị trí của C để áp lự ở đó có giá trị cực đại, cực tiểu C x O l P1 P P2 B A Bài giải: a) Trọng lượng p của thanh đặt tại trịng tâm O là trung điểm của thanh tác dụng lên hai giá đỡ A và B hai áp lực P1 và P2. Vì thanh đồng chất tiết diện đều nên ta có: do đó và (N) => b) P2 cực đại khi x = 0 do đó P2 = P = 100 N khi đó giá đỡ C trùng với tâm O l 2 cực tiểu khi x lớn nhất x = l do đó N khi giá đỡ trùng với đầu B Phần II: Bài tập mở rộng: Bài 1:a. Người ta đặt mặt lồi của một bán cầu khối lượng M trên mặt phẳng ngang như hình vẽ, tại mép của bán cầu đặt tiếp một vật nhỏ khối lượng m=300g làm cho bán cầu nghiêng đi một góc a=300 so với mặt phẳng ngang. Hãy xác định M? Biêt rằng trọng tâm của bán cầu là G nằm cách tâm cầu một đoạn OG = 3r/8 như hình 4.1.1. b. Hãy tính m khi biết M=500g, a=300. Bài 2:Một thang có trọng tâm ở chính giữa , được tựa một đầu vào tường, đầu kia trên mặt đất ( coi ma sát của tường và đất không đáng kể). Dùng một sợi dây không dãn buộc vào giữa thang ( như hình vẽ).Hỏi thang có đứng cân bằng được không? ( nói cách khác thang có bị trượt không). Bài 3: Cho hệ ròng rọc như (hình 4.1.3). a. Chứng minh rằng nếu các rònh rọc có khối lượng không đáng kể , thì không thể thiết lập được trạng thái cân bằng như hình vẽ. b. muồn hệ cân bằng như trạng thái ở hình vẽ thì khối lượng của các ròng rọc phải bằng bao nhiêu, biết rằng các ròng rọc có khối lượng như nhau.( bài 4.3/NC8) Bài 4:Cho hệ thống 4.1.4: l=50cm, R=2r=20cm. lực F vuông góc với thanh OA; dây MN quấn trên vành có bán kính R; dây SQ quấn trên vành có bán kính r. Ròng rọc O cố định, ròng rọc O' chuyển động để nâng hay hạ khối lượngm (có trọng lượng P).Hãy dùng một trong hai phương pháp khác nhau để tính F, nếu P=100N: a.Dùng quy tắc đòn bẩy b.Dùng định luật bảo toàn công. (Bài 4.4 NC8) Bài 5:Cho một tấm gỗ đồng chất, chiều dày như nhau tại mọi nơi có hình dạng là một tam giác thường. Ba người khiêng tấm gỗ để nó nằm song song mặt đất. Chứng minh rằng nếu khiêng ở 3 đỉnh của tam giác thì ba lực luôn bằng nhau. (4.5 /NC8) Bài 6:Một khối gỗ đồng chất, có chiều dày như nhau ở mọi điểm,có dạng hình thang cân :AB=2 BC=2CD=2DA=30cm, có trọng lượng P=30N đặt trên mặt bàn nằm ngang. a.Xác định trọng tâm của khối gỗ b.Cần tác dụng vào B một lực F tối thiểu là bao nhiêu để khối gỗ bắt đầu quay quanh Trục đi qua điểm C.(bài 4.6/NC8) Bài 7:Bốn người khiêng mọt tấm gỗ hình vuông ABCD, tại bốn đỉnh của nó sao cho hình vuông nằm ngang. Hình vuông có trọng lượng P=100N, đồng chất có chiều dày như nhau ở mọi điểm. Biết lực khiêng tại A là F1=10N. Tìm lực của 3 người còn lại.( bài 4.7/NC8) Bài 8:Cho thiết bị hình 4.1.8. Ròng rọc cố định có bán kính R1, ròng rọc động có bán kính R2. bỏ qua ma sát trong ròng rọc và khối lượng của chúng. Các dây căng luôn theo phương thẳng đứng. Tấm ván có trọng lượng P1; AB=l a. Dùng ngoại lực F kéo dây CD để tấm ván cân bằng (ở vị trí nằm ngang). Xác định lực F và vị trí trọng tâm của ván. b.Thay cho ngoại lực F là một người ngồi trên ván, có trọng tâm trên phương CD, kéo dây CD để ván cân bằng. Tìm tỉ số 2 bán kính để ván có thể cân bằng khi đã kéo bằng một lực hợp lý. Nếu trọng lượng ván P1=100N. trọng lượng người P2=500N. Bài 9:Một thang chiều dài l,Trọng lượng P, được tựa cân bằng vào tường nhà thật nhẵn. Thang làm với mặt đất nằm ngang một 600 Hình 4.1.9. Biết trọng tâm G của thang ở chính giữa thang. Xác định phản lực của mặt đất lên thang và của tường lên thang. Bài 10: Cho thiết bị như hình 4.1.10. Thanh cứng OA có trọng lượng không dáng kể có thể quay quanh bản lề O, vật K có trọng lượng P1, OB = 2BA. CB là một sợi dây không giản. a. Tìm lực căng dây BC và phản lực của tường lên thanh. b. Xác định vị trí cần treo vật K để Phản lực R của bản lề lên thanh cứng: b.1. Có hướng OA. b.2. Vuông góc với dây BC. c.Tìm lực căngcủa sợi dây BC trong trường hợp OA là thanh cứng, đồng chất tiết diện đều. Bài 11:Có bốn viên gạch chồng lên nhau sao cho một phần của hòn gạch trên nhô ra khỏi hòn gach dưới(hình 4.1.11). hỏi mép phải của hòn gạch trên cùng có thể nhô ra khỏi méẩiphỉ của hòn gạch dưới cùng một đoạn lờn nhất là bao nhiêu để hệ thống vẫn cân bằng. Biết chiều dài của viên gạch là l Bài 12:Một bút chì có tiết diện cắt ngang là một lục giác đều,cạnh bằng a, đặt trên mặt bàn nằm ngang. Tác dụng lên bút chì một lực F có hướng như hình vẽ 4.1.12. Tìm giá trị của hệ số ma sát K giữa bút chì và mặt bàn để: a. bút chì trượt trên mặt bàn mà không lăn. b. bút chì lăn trên mặt bàn mà không trượt. Bài 13:.Để điều chỉnh mực nước trong một bể cát rộng, người ta dùng một cơ cấu như (hình - 4.1.13).Gồm một ống trụ thẳng đứng đường kính d xuyên qua đáy bể và được đậy kín bằng một tấm kim loại đồng chất hình tròn đường kính l không chạm thành bể. Tại điểm B có bản lề nối thành ống trụ với mép tấm kim loại. Điểm mép A của đường kính AB được nối với một quả cầu rỗng, nhẹ bán kính R bằng một sợi dây mảnh không co giản, độ dài là h.Hỏi a. Khối lượng tấm kim loại phải bằng bao nhiêu đẻ khi mực nước trong bể dâng tới ngang chính giữa quả cầu thì tấm kim loại bị nâng lên và nước chảy qua ống trụ ra ngoài? biết khối lựơng riêng của nước là D0, xem tấm kim loại là khá mỏng (để có thể bỏ qua lực đẩy acsimet) . công thức tính thể tích của Hình cầu là V= 4/3 p R3. b. áp dụng số: d= 8cm, l=32cm, R=6cm, h=10cm,D0=100kg/m3.( Tuyển sinh vào chuyên lý/ ĐHTN) Bài 14:.Một ống trụ bán kính R=9cm, đặt thẳng đứng bên trong có một pít tông phẳng, một mặt dưới có gờ, nằm sát đáy bình( độ cao của gờ nhỏ không đáng kể). Môt ống trụ thành mỏng bán kính r =1cm cắm xuyên qua pít tông( hình 4.1.14). Trọng lượng của pít tông và ống trụ là P=31,4N. Đổ đều nước sạch vào bình qua ống trụ với lượng nước là 40g trong mỗi giây. Hỏi a. Nước trong ống trụ dâng lên đến độ cao h nào so với mặt dưới cuả pít tông thì pít tông bắt đầu bị đẩy lên khỏi đáy bình. b. Khi đổ hết 700g nước vào thì mặt dưới của pít tông ở độ cao nào so với đáy bình c. Vận tốc của pít tông khi nó chuyển động đều lên trên? biết khối lượng riêng của nước là D=1000kg/m3. Bỏ qua mọi ma sát. Bài 15:Cho hệ thống ròng rọc như hình vẽ 4.1.15A. muồn giữ cho P cân bằng phải léo đầu dây A xuống với một lực F=120N? Nếu treo vật P nói trên vào hệ thống ròng rọc ở ( hình 4.1.15.B thì cần phải kéo đầu dây B xuống với một lực là bao nhiêu. Bỏ qua ma sát và khối lượng của các ròng rọc. Bài 16:Hệ thống ở hình 4.1.16. đang cân bằng nếu dịch chuyển điểm treo A sang phải thì hệ thống còn thăng bằng nữa không. Bài 17:.Một tấm ván OB hình 4.1.17. trọng lượng p1 không đáng kể, đầu O tựa trên một dao cứng, đầu B được treo bằng một sợi dây vắt qua hệ thống ròng rọc. Một người có trọng lượng p2đứng trên ván tại I sao cho OA =2/3 OB kéo dây để giữ cho ván cân bằng ở vị trí nằm ngang. ( với p2>p1, bỏ qua ma sát và khối lượng của ròng rọc).hỏi a.Hỏi người đó phải kéo dây với một lưc bằng bao nhiêu . b.Lực do ván tác dụng lên dao. c. Lực do giá treo tác dụng lên ròng rọc R. Bài 18:Mặt phẳng nghiêng hình 4.1.18 có độ dài AB=1m, chiều cao AH=30cm. Vật M có khối lượng 14kg. để giữ cho vật M khỏi bị trượt xuống, người ta buộc vào nó hai sợi dây vắt qua hai ròng rọc cố định R1 vả R2 và treo hai vật nặng m1, m2. a. biết m1=4kg. Hẫy xác định m2. b. Thay m2 bằng vật nặng m3 =2,4kg. Hãy xác định m1 để vật M không trượt. c. Cho rằng hệ số ma sát giữa vật m và mặt phẳng nghiêng là k=0,05, bỏ qua ma sát ở ròng rọc. Hãy giải lại bài toán theo các yêu cầu ở câu a và câu b Bài 19: Nêu phương án xác định hàm lượng vàng và bạc trong một đồ trang sức với các dụng cụ sau:một thanh cứng ; một thước thẳng có thang đo; một vật rắn đã biết trước khối lượng;một bình nước; dây buộc đủ dùng Bài 20:Có một đồ trang sức bằng hợp kim của vàng và bạc.Hãy trình bầy phương án xác định hàm lượng phần trăm vàng , bạc trong đồ trang sức đó với các dụng cụ sau: Một cốc nước(đã biết Dn), một thanh cứng đồng chất, dây buộc ( đủ dùng và không thấm nước) thước thẳng ( hoặc thước dây) có thang đo.
Tài liệu đính kèm:
 Boi Duong HSG Ly 8.doc
Boi Duong HSG Ly 8.doc





