Các dạng bài tập môn Toán hình học 8 ban cơ bản - Chương I: Tứ giác - Năm học 2022-2023
II. ĐỊNH LÍ:
- Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua
trung điểm của cạnh thứ ba, và đường ấy cũng chính là đường trung bình của tam giác.
- Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua
trung điểm của cạnh bên còn lại và đường ấy cũng là đường trung bình của hình thang.
III, BÀI TẬP VẬN DỤNG:
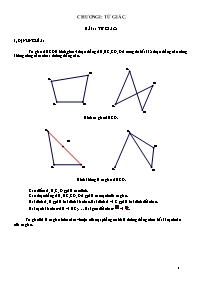
Bài 1: Để đo khoảng cách hai điểm B và C bị chắn bởi 1 cái hồ sâu, người ta thực hiện đo như hình 1. Biết khoảng cách giữa hai điểm D và E đo được là 53m, Hỏi B và C cách nhau bao nhiêu m.
Bạn đang xem 20 trang mẫu của tài liệu "Các dạng bài tập môn Toán hình học 8 ban cơ bản - Chương I: Tứ giác - Năm học 2022-2023", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
CHƯƠNG I: TỨ GIÁC. BÀI 1: TỨ GIÁC: I, ĐỊNH NGHĨA: + Tứ giác ABCD là hình gồm 4 đoạn thẳng AB, BC, CD, DA trong đó bất kì 2 đoạn thẳng nào cũng không cùng nằm trên 1 đường thẳng nào. Hình tứ giác ABCD. Hình không là tứ giác ABCD. + Các điểm A, B, C, D gọi là các đỉnh. + Các đoạn thẳng AB, BC, CD, DA gọi là các cạnh của tứ giác. + Hai đỉnh A, B gọi là hai đỉnh kề nhau. Hai đỉnh A và C gọi là hai đỉnh đối nhau. + Hai cạnh kề nhau: AB và BC; . Hai góc đối nhau: và . Tứ giác lồi là tứ giác luôn nằm về một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác. II, TỔNG CÁC GÓC CỦA MỘT TỨ GIÁC: + Tổng 4 góc trong một tứ giác bằng . Tứ giác ABCD có: + Góc ngoài của tứ giác là góc kề bù với một góc trong của tứ giác. III, BÀI TẬP VẬN DỤNG: Bài 1: Tìm số đo x trong các hình sau: Bài 2: Cho tứ giác ABCD có . Tính góc và góc ngoài tại C của tứ giác. Bài 3: Cho tứ giác ABCD có , . a, Chứng minh AC là trung trực của BD. b, Tính góc . Bài 4: Cho tứ giác ABCD có . Các tia phân giác góc A và góc B cắt nhau tại I. Biết . Tính số đo . Bài 5: Cho tứ giác ABCD. Phân giác góc và cắt nhau tại O. Chứng minh . Bài 6: Cho tứ giác ABCD, hai tia phân giác và cắt nhau tại E, hai tia phân giác góc ngoài tại A và B cắt nhau tại F. a, Chứng minh: . b, Chứng minh: . Bài 7: Cho tứ giác ABCD có , . Trên tia đối của tia DA lấy điểm E sao cho . Chứng minh: a, . b, AC là phân giác góc . BÀI 2: HÌNH THANG. I, ĐỊNH NGHĨA: + Hình thang là tứ giác có hai cạnh đối song song. Hai cạnh song song gọi là hai đáy, hai cạnh còn lại là hai cạnh bên. (H1) + Hình thang vuông là hình thang có một góc vuông. (H2) + Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. (H3) II, TÍNH CHẤT: - Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên ấy bằng nhau. - Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau. - Trong hình thang cân, hai cạnh bên bằng nhau. - Trong hình thang cân, hai đường chéo bằng nhau. III, DẤU HIỆU NHẬN BIẾT: - Hình thang có hai góc kề một đáy bằng nhau là hình thang cân. - Hình thang có hai đường chéo bằng nhau là hình thang cân. IV, BÀI TẬP VẬN DỤNG: Bài 1: Cho hình thang ABCD có AD // BC, có và . a, Tính . b, Chứng minh . c, Tính số đo các góc của hình thang. Bài 2 : Cho hình thang vuông ABCD có , , và tại H. a, Chứng minh . b, Chứng minh vuông cân tại H. Bài 3 : Cho , các tia phân giác góc cắt nhau tại I. Qua I kẻ đường thẳng song song với BC cắt AB và AC lần lượt tại D và E. a, Tìm các hình bình hành có trong hình. b, Chứng minh rằng : cân ở D và cân ở E. c, So sánh DE với tổng . Bài 4 : Cho hình thang ABCD có AB // CD và . Hai tia phân giác góc và góc cắt nhai tại K thuộc đáy AB. Chứng minh rằng : a, cân ở A, cân ở B. b, . Bài 5 : Cho hình thang ABCD có AB // CD và . Gọi K là điểm thuộc đáy CD sao cho . Chứng minh rằng : a, AK là phân giác góc . b, . c, BK là tia phân giác của góc . Bài 6 : Cho cân tại A, Hai đường trung tuyến BD và CE. Chứng minh : a, cân tại A. b, . c, Tứ giác BCDE là hình thang cân. Bài 7 : Cho cân tại A có BE và CF là hai đường phân giác. Chứng minh : a, cân tại A. b, Tứ giác BCEF là hình thang cân. c, . Bài 8: Cho hình thang cân ABCD có AB // CD và , . a, Chứng minh . b, CA có phải là tia phân giác của góc không ? Vì sao ? Bài 9: Cho hình thang cân ABCD có AB // CD và . Gọi O là giao điểm của AD và BC. E là giao điểm của AC và BD. Chứng minh : a, cân tại O. b, . c, . d, OE là trung trực của hai đáy AB và CD. Bài 10: Cho hình thang cân ABCD có AD // BC và , , . Qua B kẻ đường thẳng song song với CD cắt AD tại E. a, Tính ED. b, Chứng minh đều. c, Kẻ ở H. Tính AH. Bài 11: Cho hình thang cân ABCD có AB // CD và . AH và BK là các đường cao. Chứng minh a, . b, . Bài 12: Cho hình thang ABCD có AD // BC và . Kẻ DE // AB, ( E và H thuộc BC). Biết . a, Tính EC. b, Tính BC. c, Chứng minh . BÀI 3: ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC, HÌNH THANG. I, ĐỊNH NGHĨA: - Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác. (H4) - Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang. (H5) - Đường trung bình của tam giác thì song song với cạnh thứ 3 và bằng nửa cạnh ấy. Với H4. Ta có: - Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy. Với H5. Ta có: và II. ĐỊNH LÍ: - Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba, và đường ấy cũng chính là đường trung bình của tam giác. - Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm của cạnh bên còn lại và đường ấy cũng là đường trung bình của hình thang. III, BÀI TẬP VẬN DỤNG: Bài 1: Để đo khoảng cách hai điểm B và C bị chắn bởi 1 cái hồ sâu, người ta thực hiện đo như hình 1. Biết khoảng cách giữa hai điểm D và E đo được là 53m, Hỏi B và C cách nhau bao nhiêu m. Hình 1 Hình 2 Bài 2: Để đo khoảng cách giữa hai điểm A và B bị ngăn cách bởi một hồ nước người ta đóng các cọc tại các vị trí A, B, M, N, O như hình 2 và đo được . Tính khoản cách AB biết M, N lần lượt là điểm chính giữa OA và OB. Bài 3: Cho cân tại A, đường cao AM, N là trung điểm của AC, kẻ Ax // BC cắt MN tại E. Chứng minh: a, M là trung điểm của BC. b, ME // AB. c, . Hình bài 3 Hình bài 4 Bài 4: Cho có . Kéo dài AB lấy điểm D sao cho , Kéo dài AC lấy điểm E sao cho . Kéo dài đường trung tuyến AM của lấy . a, Tính độ dài các cạnh của . b, Chứng minh DI // BC. c, Chứng minh ba điểm D, I, E thẳng hàng. Bài 5: Cho cân tại A, có M là trung điểm của BC, kẻ Mx // AC cắt AB tại E, Kẻ My // AB cắt AC tại F. Chứng minh: a, E, F lần lượt là trung điểm của AB và AC. b, . c, . Bài 6: Cho vuông tại A có AM là đường trung tuyến. N là trung điểm của AC. a, Chứng minh . b, là tam giác gì? Vì sao? c, Chứng minh . Hình bài 5 Hình bài 6 Bài 7: Cho . Trên cạnh AB lấy . Từ D, E kẻ các đường thẳng song song với BC cắt AC lần lượt tại M, N. Chứng minh: a, M là trung điểm của AN. b, . c, . Hình bài 7 Hình bài 8 Bài 8: Cho trung tuyến AM, Trên AC lấy E và F sao cho , BE cắt AM tại O. a, Tứ giác OEFM là hình gì? Vì sao? b, Chứng minh . Bài 9: Cho , trung tuyến AM. Gọi D là trung điểm của AM, BD cắt AC tại E. Kẻ MK // BE (K thuộc EC). Chứng minh: a, K là trung điểm của CE. b, . Hình bài 9 Hình bài 10. Bài 10: Cho cân tại A có M là trung điểm của đường cao AH. CM cắt AB tại D, kẻ // CD và cắt AB tại E. Chứng minh: a, . b, . c, . BÀI 3: ĐỐI XỨNG TRỤC, ĐỐI XỨNG TÂM. HÌNH BÌNH HÀNH I, ĐỊNH NGHĨA: - Hai điểm A và A’ được gọi là đối xứng với nhau qua đường thẳng d, nếu d là đường trung trực của đoạn thẳng AA’. (H1) - Hai điểm A và A’ được gọi là đối xứng với nhau qua điểm O, nếu O là trung điểm của AA’.(H2) - Mọi điểm nằm trên đường thẳng (d) đều cách đều hai đầu mút A và A’. II. QUY ƯỚC: - Điểm nằm trên trục đối xứng (d) thì điểm đối xứng với nó qua (d) là chính nó. - Điểm đối xứng với điểm O qua tâm O chính là điểm O. III. HÌNH ĐỐI XỨNG QUA ĐƯỜNG THẲNG: - Hai hình A và B gọi là đối xứng với nhau qua đường thẳng d nếu lấy mỗi điểm thuộc hình A khi lấy đối xứng qua d đều thuộc hình B. - Hai hình A và B gọi là đối xứng với nhau qua điểm O nếu lấy mỗi điểm thuộc hình A khi lấy đối xứng qua O thì đều thuộc hình B. IV, ĐỊNH NGHĨA: - Tứ giác có các cặp cạnh đối song song là hình bình hành.( H1) - ABCD là hình bình hành: V, TÍNH CHẤT: - Trong hình bình hành các cạnh đối song song và bằng nhau. - Trong hình bình hành các góc đối bằng nhau. - Trong hình bình hành hai đường chéo cắt nhau tại trung điểm của mỗi đường. VI, DẤU HIỆU NHẬN BIẾT: - Tứ giác ABCD là HBH nếu các cạnh đối song song. - Tứ giác ABCD là HBH nếu các cạnh đối bằng nhau. - Tứ giác ABCD là HBH nếu các góc đối bằng nhau. - Tứ giác ABCD là HBH nếu hai đường chéo cắt nhau tại trung điểm của mỗi đường. - Tứ giác ABCD là HBH nếu hai cạnh đối vừa song song vừa bằng nhau. VII, BÀI TẬP VẬN DỤNG: Bài 1: Cho hình thang ABCD có AB // CD và . Gọi E là trung điểm của CD. a, Chứng minh tứ giác ABED là hình bình hành. b, Chứng minh tứ giác ABCE là hình bình hành. Bài 2: Cho có D, E, F lần lượt là trung điểm các cạnh BC, AC, AB. a, Chứng minh DE // AF và . b, Chứng minh tứ giác AEDF là hình bình hành. Bài 3: Cho cân ở A có điểm M trên cạnh BC. Kẻ MD // AC và ME // AB . a, Chứng minh ADME là hình bình hành. b, là tam giác gì? c, So sánh với AC. Hình bài 3 Hình bài 4 Bài 4: Cho cân tại A, lấy điểm D trên AB. Lấy điểm E trên tia đối của tia CA sao cho . Kẻ DF // AC . a, là tam giác gì? b, Chứng minh tứ giác DCEF là hình bình hành. Bài 5: Cho có các đường trung tuyến BE, CF và trọng tâm G. Gọi M, N lần lượt là trung điểm của BG và CG. a, Chứng minh EF // MN và . b, Chứng minh MNEF là hình bình hành. Hình bài 5 hình bài 6 Bài 6: Cho hình bình hành ABCD. Kéo dài đường trung tuyến AM của và lấy điểm E sao cho . a, Tứ giác ABEC là hình gì? b, Chứng minh D, C, E thẳng hàng và suy ra C là trung điểm của DE. Bài 7: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. a, Chứng minh MN // AC và . b, Chứng minh MN // PQ và . c, Chứng minh tứ giác MNPQ là hình bình hành. Bài 8: Cho hình bình hành ABCD. E và F lần lượt là hình chiếu của A và C trên đường chéo BD. a, Chứng minh . b, Chứng minh tứ giác AECF là hình bình hành. Bài 9: Cho hình bình hành ABCD có . Vẽ , AE kéo dài cắt CD tại H và CF kéo dài cắt AB tại K. Chứng minh: a, AECF là hình bình hành. b, AHCK là hình bình hành. Bài 10: Cho hình bình hành ABCD. Kẻ và . a, Tứ giác AECF là hình gì? Vì sao? b, AE cắt CD tại I, CF cắt AB tại K. Chứng minh . c, Chứng minh . Bài 11: Cho hình bình hành ABCD có . Tia phân giác góc cắt BC ở I, tia phân giác góc cắt AD tại K. Chứng minh: a, là tam giác cân. b, So sánh và . c, Tứ giác AICK là hình bình hành. Bài 12: Cho hình bình hành ABCD có M, N lần lượt là trung điểm của AB và CD. Nối AN và CM cùng cắt BD lần lượt ở E và F. Chứng minh: a, và tứ giác AMCN là hình bình hành. b, F là trung điểm của BE và E là trung điểm của DF. Bài 13: Cho hình bình hành ABCD, Trên cạnh AB lấy điểm M, trên cạnh CD lấy điểm N sao cho a, Chứng minh rằng: . b, Chứng minh tứ giác AMCN là hình bình hành. c, Chứng minh tứ giác BMDN là hình bình hành. Bài 14: Cho hình bình hành ABCD, Trên cạnh AB lấy điểm E, trên cạnh CD lấy điểm F sao cho . Gọi O là giao điểm của AC và BD. a, Chứng minh tứ giác AECF là hình bình hành. b, Chứng minh O là trung điểm của EF. Bài 15: Cho hình bình hành ABCD. Gọi H và K lần lượt là hìn ... K là hình thoi. b, Chứng minh tứ giác AKMB là hình bình hành. c, Tìm điều kiện của để tứ giác AMCK là hình vuông. Bài 5: Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, trên cạnh CD lấy điểm N sao cho . Chứng minh rằng: a, . b, . Bài 6: Cho hình vuông ABCD. Trên cạnh AD lấy điểm F, Trên cạnh DC lấy điểm E sao cho . Chứng minh: a, . b, . c, . Bài 7: Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lấy lần lượt các điểm M, N, P, Q sao cho . a, Chứng minh . b, Chứng minh . c, Chứng minh MNPQ là hình vuông. Bài 8: Cho hình vuông ABCD. Gọi E, F, K lần lượt là trung điểm của AB, BC, CD. a, Chứng minh: AECK là hình bình hành. b, Chứng minh tại M. c, AK cắt DF tại N. Chứng minh N là trung điểm của DM. d, Chứng minh . Bài 9: Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, Qua A kẻ ( điểm N thuộc tia đối của tia DC). Gọi I là trung điểm của MN. Chứng minh rằng: a, . b, Ba điểm B, I, D thẳng hàng. Bài 10: Cho hình bình hành ABCD. Gọi DE, BK lần lượt là đường phân giác của . a, Chứng minh DE // BK. b, Cho . Chứng minh . c, Trong trường hợp . Tìm số đo để tứ giác DEBK là hình vuông. Bài 11: Cho hình bình hành ABCD có . Gọi M, N theo thứ tự là trung điểm của AB, CD. a, Chứng minh . b, Tứ giác AMCN là hình gì? Vì sao? Bài 12: Cho hình bình hành ABCD có . M là trung điểm của BC. Trên tia đối của tia MA lấy . Chứng minh: a, Tứ giác ABEC là hình thoi. b, D, E, C thẳng hàng. c, C là trung điểm của DE. Bài 13: Cho hình bình hành ABCD có . Gọi M, N lần lượt là trung điểm của AB và CD. a, Chứng minh . b, Chứng minh . c, Chứng minh tứ giác AMCN là hình thoi. Bài 14: Cho hình chữ nhật ABCD. Tia phân giác góc cắt tia phân giác góc tại F. Tia phân giác góc cắt tia phân giác góc tại E. a, Tính các góc của . b, Chứng minh . c, BE cắt CF tại H. Chứng minh . Bài 15: Cho hình chữ nhật ABCD có . Gọi I là trung điểm của AB và K là trung điểm của DC. Chứng minh: a, và là hình vuông. b, và . Bài 16: Cho hình chữ nhật ABCD có . Gọi I là trung điểm của AB và K là trung điểm của DC. a, Chứng minh tứ giác AIKD và BIKC là hình vuông b, Chứng minh vuông cân. c, Gọi S và R lần lượt là tâm các hình vuông AIKD và BIKC. Chứng minh ISKR là hình vuông. Bài 17: Cho hình bình hành ABCD có . Gọi P và Q lần lượt là trung điểm của AB và CD. a, Chứng minh tứ giác APCQ là hình bình hành. b, Chứng minh tứ giác APQD là hình thoi. c, Gọi E là giao điểm của AQ và DP, Gọi F là giao điểm của BQ và CP. Chứng minh tứ giác PEQF là hình chữ nhật. d, Hình bình hành ABCD cần có thêm điều kiện gì để PEQF là hình vuông. Bài 18: Cho hình bình hành ABCD có . Gọi M và N là trung điểm của AB và CD. a, Tứ giác AMND là hình gì? b, Chứng minh AN // MC. c, E là giao điểm của AN và DM. F là giao điểm của MC với BN. Chứng minh EF // DC. d, Tứ giác MENF là hình gì? e, Tìm điều kiện của hình bình hành ABCD để tứ giác MENF là hình vuông. Bài 19: Cho hình bình hành ABCD có . Gọi E là chân đường vuông góc kẻ từ C đến đường thẳng AB, M là trung điểm của AD, F là chân đường vuông góc kẻ từ M đến CE và MF cắt BC ở N. a, Tứ giác MNCD là hình gì? Vì sao? b, là tam giác gì? Vì sao? c, Chứng minh rằng: . Bài 20: Cho hình thoi ABCD có . Kẻ , rồi kéo dài một đoạn . Nối E với A, E với D. Chứng minh: a, H là trung điểm của AD. b, Tứ giác ABDE là hình thoi. c, D là trung điểm của CE. d, . Bài 21: Cho , các đường trung tuyến BD và CE cắt nhau tại G. Gọi M là trung điểm của GB, N là trung điểm của GC. a, Tứ giác DEMN là hình gì? Vì sao? b, Để tứ giác DEMN là hình chữ nhật thì phải có thêm điều kiện gì? c, cần thêm điều kiện gì để DEMN là hình vuông? Bài 22: Cho các đường trung tuyến BD và CE cắt nhau ở G. Gọi H là trung điểm của GB, K là trung điểm của GC. a, Chứng minh tứ giác DEHK là hình bình hành. b, Nếu cân tại A. Chứng minh: và là hình chữ nhật. c, Nếu các đường trung tuyến . Khi đó tứ giác DEHK là hình gì? Vì sao? Bài 23: Cho vuông cân tại B. a, Gọi D là điểm đối xứng với C qua B. Chứng minh vuông cân. b, Gọi BE và BF lần lượt là đường phân giác trong của và . Chứng minh BA là phân giác của . c, Chứng minh AEBF là hình vuông. d, So sánh với . Bài 24: Cho vuông tại A. Từ một điểm M trên cạnh BC. Kẻ tại H. Kẻ tại K. a, Chứng minh: Tứ giác AHMK là hình chữ nhật. b, Tìm vị trí của M trên cạnh BC để AHMK là hình vuông. c, Kẻ tại I. So sánh AM với AI rồi tìm vị trí của M để nhỏ nhất. Bài 25: Cho vuông tại D có , DM là đường trung tuyến. Gọi MN là đường vuông góc kẻ từ M đến DE, MK là đường vuông góc kẻ từ M đến DF. Gọi H là điểm đối xứng với M qua N. a, Tứ giác DKMN là hình gì? Vì sao? b, Gọi O là trung điểm của DM. Chứng minh 3 điểm H, O, F thẳng hàng. c, cần thêm điều kiện gì để tứ giác DKMN là hình vuông. Bài 26: Cho hình thoi ABCD có . Gọi M, N lần lượt trên AB, BC sao cho . a, Chứng minh . b, Chứng minh là tam giác đều. Bài 27: Cho hình thoi ABCD. Lấy E và F trên BC và CD sao cho . Gọi G và H lần lượt là giao điểm của AE, AF với BD. Chứng minh tứ giác AGCH là hình thoi. Bài 28: Cho . Lấy các điểm D và E lần lượt trên AB và AC sao cho . Gọi M, N, I, K lần lượt là trung điểm của BE, CD, DE và BC. Chứng minh: a, . b, . Bài 29: Cho hình thang cân ABCD ( AB // CD). Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA. Chứng minh tứ giác MNPQ là hình thoi. Bài 30: Cho hình thang ABCD ( AB // CD). Gọi M, N, P, Q lần lượt là trung điểm của AD, AB, BC, CD. a, Chứng minh MNPQ là hình bình hành. b, Hình bình hành MNPQ là hình gì nếu hai đường chéo và . Bài 31: Cho hình thoi ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. a, Chứng minh . b, Tứ giác MNPQ là hình chữ nhật. Bài 32: Cho hình thoi ABCD có O là giao điểm của hai đường chéo. Gọi E, F, G, H lần lượt là chân đường vuông góc tự O xuống AB, BC, CD, DA. a, Chứng minh E, O, G thẳng hàng và H, O, F thẳng hàng. b, Chứng minh . c, Tứ giác EFGH là hình gì? Vì sao? Bài 33: Cho hình thoi ABCD ( góc tù). Từ B hạ . Từ D hạ . Gọi H là giao điểm của MB và PD, K là giao điểm của BN và DQ. O là giao điểm của AC và BD. Chứng minh: a, H là trực tâm . b, A, H, K, C thẳng hàng. c, . d, . e, Tứ giác BHDK là hình thoi. Bài 34: Cho hình bình hành ABCD. Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng m đi qua O cắt AB và CD lần lượt tại M và P. đường thẳng n đi qua O cắt cạnh BC và DA lần lượt tại N và Q. Biết . a, Chứng minh MNPQ là hình bình hành. b, Chứng minh MNPQ là hình thoi. Bài 35: Cho hình vuông ABCE. Hai đường thẳng m và n vuông góc với nhau ở tâm O của hình vuông. Đường thẳng m cắt AB, CD lần lượt ở P và Q. đường thẳng n cắt BC và AD ở R và S. a, Chứng minh . b, Chứng minh . c, Tứ giác PRQS là hình vuông. Bài 36: Cho hình vuông ABCD. Trên cạnh DC lấy điểm E. Từ A dựng đường thẳng vuông góc với AE tại A, đường thẳng này cắt đường thẳng BC tại F. a, Chứng minh . b, Từ E dựng đường thẳng song song với AF và từ F dựng đường thẳng song son với AE, hai đường thẳng này cắt nhau tại G. Chứng minh BD, AG, EF đồng quy. Bài 37: Cho hình vuông ABCD. Vẽ . Tia Ax cắt BC ở M, Ay cắt đường thẳng CD tại N. a, Chứng minh vuông cân. b, Vẽ hình bình hành MANF có O là giao điểm của AF và MN. Chứng minh D, O, B thẳng hàng. c, Chứng minh . Bài 38: Cho hình vuông ABCD. Trên tia đối của tia CB lấy điểm M, Trên tia đối của tia DC lấy điểm N sao cho . Vẽ hình bình hành MANF. Gọi O là trung điểm của AF. Chứng minh rằng: a, Tứ giác MANF là hình vuông. b, F thuộc tia phân giác góc . c, . d, Tứ giác BOFC là hình thang. Bài 39: Cho hình vuông ABCD, Kéo dài BC lấy điểm E, Kéo dài CD lấy điểm F sao cho . a, Chứng minh . b, là tam giác gì? Vì sao? c, Kẻ tia Ex // AF và tia Fy // AE. Ex cắt Fy tại G. Tứ giác AEGF là hình gì? Vì sao? Bài 40: Cho hình vuông ABCD. Trên tia đối của các tia AD, BA, CB, DC lần lượt lấy các điểm A’, B’, C’, D’. sao cho . Chứng minh: a, . b, . c, Tứ giác là hình vuông. Bài 41: Cho hình vuông ABCD. Từ điểm M thuộc cạnh BC vẽ đường thẳng cắt CD ở K sao cho . Kẻ ở H. Chứng minh: a, và . b, . c, . Bài 42: Cho hình vuông ABCD. M là điểm tùy ý trên cạnh DC. Tia phân giác của cắt CD tại I. Kẻ tại H và tia IH cắt BC tại K. Chứng minh: a, . b, . c, . Bài 43: Cho hình vuông ABCD. Trong hình vuông vẽ đều. Bên ngoài hình vuông vẽ đều. a, Tính các góc của . b, Chứng minh vuông cân. c, Chứng minh A, E, F thẳng hàng. Bài 44: Cho vuông tại A, . Gọi E là trung điểm của AC, M là trung điểm của BC. a, Tính EM. b, Vẽ tia Bx // AC sao cho Bx cắt EM tại D. Chứng minh rằng tứ giác ABDE là hình vuông. c, Gọi I là giao điểm của BE và AD. Gọi K là giao điểm của BE với AM. Chứng minh rằng tứ giác BDCE là hình bình hành và . Bài 45: Cho hình thang vuông ABCD có AB // CD và . Có . Gọi E là điểm đối xứng của A qua B. a, Chứng minh và tứ giác AECD là hình vuông. b, Gọi M là trung điểm của EC và I là giao điểm của BC và DM. Chứng minh diện tích bằng diện tích tứ giác . c, Biết DA và CB cắt nhau tại V. Gọi N là hình chiếu của I trên AD. Chứng minh . Bài 46: Cho cân tại B có đường cao BE. Trên tia đối của tia EB lấy điểm D sao cho . a, Chứng minh tứ giác ABCD là hình bình hành. b, Chứng minh tứ giác ABCD là hình thoi. Bài 47: Cho cân tại A, có đường cao AH. a, Tính diện tích biết . b, Gọi M là trung điểm của AB và E là điểm đối xứng của H qua M. Chứng minh tứ giác AHBE là hình chữ nhật. c, Gọi F là điểm đối xứng của A qua H. Chứng minh tứ giác ABFC là hình thoi. d, Kẻ , Gọi I, Q lần lượt là trung điểm của HK, KC. Chứng minh . Bài 48: Cho hình vuông ABCD có O là giao của hai đường chéo. Lấy Q là điểm bất kì trên đường chéo BD ( Q khác B và D). Gọi E, F theo thứ tự là hình chiếu vuông góc của Q trên AB, AD. a, Chứng minh tứ giác AEQF là hình chữ nhật. b, Chứng minh và tính . c, Gọi M, K lần lượt là trung điểm của AB, OD. Tính . Bài 49: Cho hình vuông ABCD. Qua A vẽ hai đường thẳng vuông góc với nhau lần lượt cắt BC tại P và R. Cắt CD tại Q và S. a, Chứng minh và là các tam giác cân. b, QR cắt PS tại H. Hai điểm M, N lần lượt là trung điểm của QR và PS. Chứng minh tứ giác AMHN là hình chữ nhật. c, Chứng minh P là trực tâm . d, Chứng minh MN là đường trung trực của AC. e. Chứng minh bốn điểm M, B, N, D thẳng hàng. Bài 50: Cho đoạn thẳng AB và một điểm M thay đổi trên đoạn AB ( M không trùng với A và B) Vẽ các hình vuông AMCD và BMEF thuộc cùng một nửa mặt phẳng với bờ AB. a, Chứng minh và . b, Gọi G, I, N, K lần lượt là trung điểm của AB, AC, CE, EB. Tứ giác GINK là hình gì? Vì sao? c, Chứng minh DF luôn đi qua 1 điểm cố định khi M di chuyển trên AB. d, Chứng minh rằng trung điểm Q của IK luôn nằm trên một đường cố định khi M di chuyển trên AB.
Tài liệu đính kèm:
 cac_dang_bai_tap_mon_toan_hinh_hoc_8_ban_co_ban_chuong_i_tu.docx
cac_dang_bai_tap_mon_toan_hinh_hoc_8_ban_co_ban_chuong_i_tu.docx





