Bồi dưỡng học sinh giỏi Hình học 8 - Chuyên đề: Tìm lời giải bằng vẽ thêm đường phụ - Tạ Phạm Hải
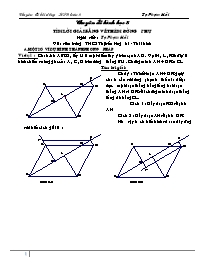
ở hình 1a : Để chứng minh PH = CL bằng cách chứng minh vPHK = vCLB
ở hình 1b : Để chứng minh AP = CL ta cần chứng minh vAPD = vCLB
ở hình 2 a : Ta cần chứng minh vBLC = vAPD
ở hình 2 b : Ta cần chứng minh vBLC = v HKP
Bạn đọc tự chứng minh .
Tuy nhiên nếu biến đổi kết luận về dạng hiệu là : AH = CL – DK hoặc DK = CL – AH
thì bằng cách vẽ tạo ra các đoạn thẳng hiệu và ta lại có thêm những cách giải khác theo các hình vẽ sau :
Tóm lại có 8 cách giải như trên .
Bạn đọc tự trình bày lời giải .
Ví dụ 2 : Cho ABC có AB > AC và góc A bằng 0 . Trên cạnh AB lấy điểm D sao cho BD = AC . Gọi E và F thứ tự là trung điểm của các đoạn thẳng AD , BC . Tính góc BEF theo .
Tìm lời giải :
Câu hỏi đặt ra là làm thế nào để tìm hoặc tạo ra các mối quan hệ giữa các góc BEF và góc BAC ? Cần vẽ đường phụ như thế nào ?
Để ý rằng AC = BD , Hãy tìm cách vẽ đẩy chúng về phía nhau , làm xuất hiện các tam giác
Chuyên đề hình học 8 tìm lời giải bằng vẽ thêm đường phụ Người viết : Tạ Phạm Hải Giáo viên trường THCS Thị trấn Hưng hà - Thái bình A.Một số ví dụ hình thành phương pháp Ví dụ 1 : Cho h.b.h ABCD , lấy M là một điểm tùy ý trên cạnh AD . Gọi H , L , K thứ tự là hình chiếu vuông góc của A , C , D trên đường thẳng BM . Chứng minh AH + DK = CL Tìm lời giải : Chú ý : Từ kết luận AH + DK gợi ý cho ta cần vẽ đường phụ như thế nào để tạo được một đoạn thẳng bằng tổng hai đoạn thẳng AH và DK rồi chứng minh đoạn thẳng tổng đó bằng CL. Cách 1 : Đẩy đoạn KD về phía AH Cách 2 : Đẩy đoạnAH về phía DK Như vậy ta có bốn hình vẽ sau đây ứng với bốn cách giải là : ở hình 1a : Để chứng minh PH = CL bằng cách chứng minh rvPHK = rvCLB ở hình 1b : Để chứng minh AP = CL ta cần chứng minh rvAPD = rvCLB ở hình 2 a : Ta cần chứng minh rvBLC = rvAPD ở hình 2 b : Ta cần chứng minh rvBLC = rv HKP Bạn đọc tự chứng minh . Tuy nhiên nếu biến đổi kết luận về dạng hiệu là : AH = CL – DK hoặc DK = CL – AH thì bằng cách vẽ tạo ra các đoạn thẳng hiệu và ta lại có thêm những cách giải khác theo các hình vẽ sau : Tóm lại có 8 cách giải như trên . Bạn đọc tự trình bày lời giải . Ví dụ 2 : Cho rABC có AB > AC và góc A bằng a0 . Trên cạnh AB lấy điểm D sao cho BD = AC . Gọi E và F thứ tự là trung điểm của các đoạn thẳng AD , BC . Tính góc BEF theo a . Tìm lời giải : Câu hỏi đặt ra là làm thế nào để tìm hoặc tạo ra các mối quan hệ giữa các góc BEF và góc BAC ? Cần vẽ đường phụ như thế nào ? Để ý rằng AC = BD , Hãy tìm cách vẽ đẩy chúng về phía nhau , làm xuất hiện các tam giác cân ; hoặc vẽ hình để lợi dụng yếu tố trung điểm mà đề bài đã cho . Đẩy BD về phía AC ta được hình 1; 4 ; 6 và ngược lại ta được hình 2 ; 3 ; 5 Tóm tắt lời giải cho hình 1: Trên tia đối của tia AB lấy điểm K sao cho AK = BD = AC , ị E là trung điểm của đoạn thẳng BK ; rACK cân tại A và EF là đường trung bình của rBCK . Ta được góc BEF bằng góc AKC và bằng 1/2 số đo của góc BAC . Vậy góc BEF bằng a/2. Tóm tắt lời giải cho hình 2 : Lấy P đối xứng với C qua điểm E thì tứ giác ACDP la hình bình hành , ị rPBD cân tại D . Ta có góc ADP bằng a ( so le trong ) và góc ADP bằng hai lần góc DBP ( quan hệ góc trong và góc ngoài của rDPB ) . Lại có góc DBP bằng góc BEF ( so le trong ). Vậy BEF bằng a / 2 . Tóm tắt lời giải cho hình 5 : Dựng hình bình hành ACBK ị rBDK cân tại B . Gọi H là trung điểm của DK thì BH là phân giác của góc DBK . Vậy góc EBH = 1/2 góc EBK = a/2 = góc BEF ( so le trong ) Bạn đọc hãy tìm lời giải cho hình 3 và 4 , 6 Lợi dụng yếu tố trung điểm mà đề bài đã cho Tóm tắt lời giải cho hình 7 : Trên tia đối của tia AC lấy điểm P sao cho PA = BA , ta được rABP cân tại A . Gọi Q là trung điểm của đoạn CP thì CQ = CP/2 = ( AB + AC )/ 2 = BE . Từ đó AQ = AE = DE và rAQE cân tại A và ba điểm E , F , Q thẳng hàng . Từ đây dẽ dàng tính được góc BEF bằng a / 2 . Ví dụ 3 : Cho hình chữ nhật ABCD . Gọi H là hình chiếu vuông góc của A trên BD ; I và J thứ tự là trung điểm của các đoạn thẳng DH và BC . Tính số đo cú góc AIJ . Tìm lời giải Từ hình vẽ ( khá chính xác ) ta dự đoán góc AIJ = 900.Dựa vào yếu tố trung điểm mà đề đã cho mà vẽ thêm hình tạo sự liên kết giữa I và J . Cách 1 : ( hình 1,2) Vẽ hình phụ khai thác yếu tố trung điểm Cách 3 ( hình 3 , 4 ) Vẽ hình phụ tạo các tam giác đồng dạng để xét các quan hệ về góc Tóm tắt lời giải cho hình 1 Gọi P là trung điểm của AH thì IP ^ AB và P là trực tâm của rABI . Từ đó tứ giác BPIJ là h.b.h ,ị BP // IJ mà BP ^ AI nên JI ^ AI . Tóm tắt lời giải cho hình 4 ( xem hình vẽ ) Vì góc DAH = góc ACB < 900 nên rvAHD ~ rvABC ị nên lại có rv AHI ~ rvABJ . Ta được ịrAOI ~ rBOJ ( g – g ) ị rAOB ~ rIOJ ( c – g – c ) nên góc JAB = góc JIB = góc IAH mà góc AIH + góc IAH = 900 nên góc AIH + góc JIB = 900 . Hay góc AIJ = 900 .( Với lớp 9 nên dùng tứ giác nội tiếp với hình 4 ) Bạn đọc tự giải cho hình 2 và hình 3 . Qua các ví dụ trên có thể rút ra một kết luận là : Thông thường cách vẽ đường phụ xuất phát từ cách tìm kiếm lời giải bằng phân tích đi lên Vẽ đường phụ để liên kết những yếu tố đã cho với nhau : Đẩy chúng về phía nhau , tạo ra hình trung gian Vẽ đường phụ để khai thác hoặc tạo thêm giả thiết ( dựa vào kiến thức đã học ) Vẽ đường phụ để sử dụng một phương pháp nào đó đặc biệt để giải : Phương pháp tam giác đồng dạng , phương pháp diện tích ; phương pháp tứ giác nội tiếp ( lớp 9 ) hoặc phương pháp đại số v. v . B . Bài tâp luyện tập Bài tập 1 : Cho góc vuông xOy . Trên tia Ox lấy điểm B và trên tia Oy theo thứ tự lấy các điểm C , D , E sao cho C nằm giữa O và D , D nằm giữa C và E ,và đồng thời thỏa mãn : OC = CD = DE = OB Tính tổng của các góc ODB và góc OEB Bài tập 2 : Cho hình vuông ABCD . Lấy M , N thứ tự là trung điểm của các cạnh AD , AB . Các đoạn thẳng CM và DN cắt nhau tại P . Chứng minh rPBC cân Bài tập 3 : Độ dài đường trung bình của một hình thang là 40 cm . Hai góc kề đáy nhỏ ( góc trong ) bằng 1300 và 1400 . Hãy tìm độ dài mỗi cạnh của hình thang biết rằng độ dài của đoạn thẳng nối trung điểm hai đáy của hình thang đó bằng 1 cm. Bài tập 4 : Cho hình vuông ABCD , lấy điểm M tùy ý trong đoạn BC . Tia kẻ từ A và vuông góc với AM cắt đường thẳng CD tại E ; EM cắt BD tại H . Chứng minh AH^ EM .
Tài liệu đính kèm:
 Chuyen de hinh 8 Ve duong phu.doc
Chuyen de hinh 8 Ve duong phu.doc





