Bài tập tự luận Hình học Lớp 8
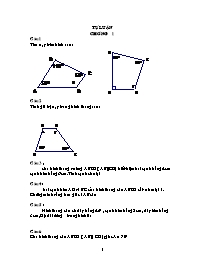
Câu 3 :
cho hình thang vuông ABCD ( AB//CD) biết hiệu hai cạnh bằng 4cm cạnh bên bằng 6cm. Tính cạnh còn lại
Câu 4:
hai cạnh bên AD và BC của hình thang cân ABCD cắt nhau tại I. Chứng minh rằng tam giác IAB cân
Câu 5 :
Hình thang cân có đáy bằng 450 , cạnh bên bằng 2cm, đáy lớn bằng 3cm, Độ dài đường trung bình là:
Câu 6
Cho hình thang cân ABCD ( AB // CD); góc A = 700
a) Tính các góc của hình thang
b) Kẻ đường cao DH và CK của hình thang. Chứng minh DH = CK
câu 7:
Cho tam giác ABC cân tại A. Trên các cạnh AB, AC lấy theo thứ tự các điểm D và E sao cho AD = AE.
Chứng minh BDEC là hình thang cân
Câu 8
cho hình thang cân , gọi O là giao điểm hai đường chéo. Chứng minh rằng: OA=OB; OC=OD
Bạn đang xem tài liệu "Bài tập tự luận Hình học Lớp 8", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
Tự luận Chương 1 Câu 1 Tìm x, y trên hình sau: Câu 2 Tính giá trị x, y trong hình thang sau: Câu 3 : cho hình thang vuông ABCD ( AB//CD) biết hiệu hai cạnh bằng 4cm cạnh bên bằng 6cm. Tính cạnh còn lại Câu 4: hai cạnh bên AD và BC của hình thang cân ABCD cắt nhau tại I. Chứng minh rằng tam giác IAB cân Câu 5 : Hình thang cân có đáy bằng 450 , cạnh bên bằng 2cm, đáy lớn bằng 3cm, Độ dài đường trung bình là: Câu 6 Cho hình thang cân ABCD ( AB // CD); góc A = 700 a) Tính các góc của hình thang b) Kẻ đường cao DH và CK của hình thang. Chứng minh DH = CK câu 7: Cho tam giác ABC cân tại A. Trên các cạnh AB, AC lấy theo thứ tự các điểm D và E sao cho AD = AE. Chứng minh BDEC là hình thang cân Câu 8 cho hình thang cân , gọi O là giao điểm hai đường chéo. Chứng minh rằng: OA=OB; OC=OD Câu 9 cho tam giác vuông ABC ( Â=900) , BC=2AB; kẻ trung tuyến AD đường cao AH. Tia Hx song song AD cắt AB ở E. Qua D dựng DF vuông góc AC ( F thuộc AC) chứng minh: tứ giác HDAE là hình thang cân Câu 10: Cho tam giác ABC có BC = 4cm. Gọi D, E theo thứ tự là trung điểm của AB, AC; M, N theo thứ tự là trung điểm của BD và CE. Tính độ dài đoạn MN? Câu 11: Cho hình thang ABCD ( AB // CD). M là trung điểm của AD, N là trung điểm của BC. Gọi I là giao điểm của MN và BD. Cho AB = 6cm; CD = 14cm. Tính độ dài đoạn MI, NI? Câu 12 Cho tứ giác ABCD. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng tứ giác EFGH là hình gì? Câu 13 cho tam giác vuông ABC ( Â=900) , BC=2AB; kẻ trung tuyến AD đường cao AH. Tia Hx song song AD cắt AB ở E. Qua D dựng DF vuông góc AC ( F thuộc AC) chứng minh: Tứ giác AEDF là hình bình hành Câu 14 cho tam giác ABC các đường trung tuyến AD, BE,CF. qua F kẻ đường thẳng song song bới BE cắt AD ở G. chứng minh: Tứ giác AFEG là hình bình hành Câu 15 Cho góc vuông xOy, điểm M nằm trong góc đó. Gọi N là điểm đối xứng với M qua Ox, P là điểm đối xứng với M qua Oy. Chứng minh rằng P và N đối xứng nhau qua O. Câu 16 cho tam giác ABC các đường trung tuyến AD, BE,CF. qua F kẻ đường thẳng song song bới BE cắt AD ở G. chứng minh: CG=AD Câu 17 Tính x trên hình vẽ sau( đơn vị đo :cm) Câu 18 Cho MNP ,điểm A di chuyển trên cạnh NP. Gọi K là trung điểm của MA. Điểm K di chuyển trên đường nào ? Câu 19 Cho hình thoi ABCD có 2 đường chéo có độ dài lần lượt bằng 10cm, 12cm. Tính cạnh của hình thoi? Câu 20: Cho tứ giác ABCD. Gọi E, F, G ,H theo thứ tự là trung điểm của AB, BC, CD, DA. Các đường chéo củÂC, BD của tứ giác có điều kiện gì thì EFGH là hình chữ nhật. Chương 2 Câu 21 a/ Cho hình thoi ABCD có góc A bằng 600 gọi M, N, E, F là trung điểm của AB, BC, CD, DA. Chứng minh đa giác MBNEDF là hình lục giác đều. b/ Tính số cạnh của đa giác biết rằng tổng số đa của các góc trong và góc ngoài của đa giác là 10800 Câu 22 a/ Tính các cạnh của hình chữ nhật biết bình phương một cạnh là 16cm2 và diện tích hình chữ nhật là 20cm2 b/ ABCD là hình vuông cạnh bằng 15cm. Tính x sao cho diện tích tam giác ADE bằng diện tích hình vuông ABCD. Câu 23 Tớnh diện tớch hỡnh thang vuụng ABCD (AB//CD) biết AB=2cm ;CD=4Cm; C = 450 Câu 24 Tớnh diện tớch hỡnh thoi ABCD Cú AB= 6cm , ABC=1200 Câu 25 Cho hình thoi ABCD, biết AB=5cm , AI=3cm (I là giao điểm của 2 đường chéo ) .Hãy tính diện tích hình thoi đó. Chương3 định lý Talét bài 1: cho hình thoi BEDF nội tiết tam giác ABC( E thuộc AB, Dthuộc AC, F thuộc BC) Tính các cạnh hình thoi biết : AB=c, BC=a chứng minh BD < bài2 Cho tam giác ABC có AC>AB, AC=45, Hình chiếu của AC và BC trên BC theo thứ dài 27cm và 15cm. đường trung trực của BC cắt AC tại N. Tính CN bài 3 Cho tam giác ABC vuông tại A. vẽ ra ngoài tam giác đó các tam giác ABD cân tại B, ACF cân tại C. Gọi H là giao điểm của AB và CD, K là giao của AC và BF. Chứng minh: a/ AH=AK b/AH2=BH.CK Bài 4 Một đường thẳng qua đỉnh A của hình bình hành ABCD cắt BD,BC,DC theo thứ tự tại E,K,G .Chứng minh rằng: a/ AE2=EK.EG b/ bài 5 Cho tứ giác lồi ABCD. Đường thẳng qua A với BC cắt BD ở E. Đường thẳng qua B song song với AD cắt AC ở G. a/ Chứng minh EG// DC b/ Giả sử AB//CD. Chứng minh rằng AB2=EG.DC bài 6 Cjo tam giác ABC, trung tuyến AM. các tia phân giác của các góc AMB và AMC cắt AB,AC tại D,E a/ chứng ming rằng: DE//BC b/ cho BC=a, AM=m. tính DE c/ Tìm tập hợp giao điiểm I của AM và DE biết cạnh BC không đổi và trung tuyến AM có độ dài bằng m d/ Tam giác ABC có điều kiện gì thì thì DE là đường trung bình của tam giác ABC Bài 7 Trên cạnh huyền BC của tam giác vuông ABC lấy điểm D sao cho AD=AC. Gọi E là điểm đối xứng của D qua C a/ CMR tam giác ABD đồng dạng với tam giác EBA b/ CM định lý Pitago bài 8 Tam giác ABC cân tại A có BC=6cm. M là trung điểm của BC. Lấy D,E lần lượt thuộc các cạnh AB và AC sao cho góc DME bằng góc B a/ CM tam giác BDM đồng dạng với tam giác CME b/ CMR tích BD.CE không đổi c/ CMR DM là tia phân giác góc BDE d/ tính chu vi tam giác AED nếu tam giác ABC là tam giác đều Câu 18: Cho tam giác ABC,trong đó AB=15(cm), AC=20(cm). trên hai cạnh AB và AC lần lượt lấy hai điểm D và E sao cho AD=8(cm), AE= 6(cm). hai tam giác ABC và AED có đồng dạng với nhau không? vì sao? Câu 19: Cho tam giác vuông, trong đó cạnh huyền dài 20(cm) và một cạnh góc vuông dài 12(cm). Tính độ dài hình chiếu cạnh góc vuông kia trên cạnh huyền Câu 20: Chân đường cao AH của tam giác vuông ABC chia cạnh huyền BC thành hai đoạn thẳng có độ dài 25cm và 36cm. tính chu vi và diện tích tam gíac vuông đó Câu 21: Tam giác ABC có độ dài các cạnh lần lượt là: 3cm, 4cm, 5cm. tam giác MNP đồng dạng tam giác ABC và có diện tích là 54cm2. Tính độ dài các cạnh của tam giác MNP. Câu 22: Cho hình hộp chữ nhật ABCD.A1B1C1D1 có AB = 6cm, BB1= 5cm, CB = 4 cm. Gọi E,F,G,H lần lượt là trung điểm của AB, DC, D1C1, A1B1 Có bao nhiêu đường thẳng song song với mp(EFGH) ? Có những mặt phẳng nào song song với nhau ?
Tài liệu đính kèm:
 bai tap tu luan hinh 8.doc
bai tap tu luan hinh 8.doc





