Bài tập ôn bồi dưỡng hình học Lớp 8 - Năm học 2011-2012
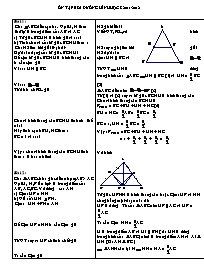
Bài 1:
Cho ABC đều cạnh a. Gọi M, N theo thứ tự là trung điểm của AB và AC
a) Tứ giác BCMN là hình gì? vì sao?
b) Tính chu vi của tứ giác BCNM theo a
Cho HS tìm lời giải ít phút
Dự đoán dạng của tứ giác BCNM?
Để c/m tứ giác BCNM là hình thang cân
ta cần c/m gì?
Vì sao MN // BC
Vì sao ?
Từ đó ta có KL gì?
Chu vi hình thang cân BCNM tính nh thế nào?
Hãy tính cạnh BM, NC theo a
BC = ? vì sao?
Vậy: chu vi hình thang cân BCNM tinh theo a là bao nhiêu?
Bạn đang xem tài liệu "Bài tập ôn bồi dưỡng hình học Lớp 8 - Năm học 2011-2012", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
ễN TẬP BỒI DƯỠNG HèNH HỌC 8 2011-2012 Bài 1: Cho ABC đều cạnh a. Gọi M, N theo thứ tự là trung điểm của AB và AC a) Tứ giác BCMN là hình gì? vì sao? b) Tính chu vi của tứ giác BCNM theo a Cho HS tìm lời giải ít phút Dự đoán dạng của tứ giác BCNM? Để c/m tứ giác BCNM là hình thang cân ta cần c/m gì? Vì sao MN // BC Vì sao ? Từ đó ta có KL gì? Chu vi hình thang cân BCNM tính như thế nào? Hãy tính cạnh BM, NC theo a BC = ? vì sao? Vậy: chu vi hình thang cân BCNM tinh theo a là bao nhiêu? Bài 2: Cho ABC có ba góc đều nhọn; AB > AC Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Vẽ đường cao AH a) C/m: MP = NH b) Giả sử: MH PN. C/m: MN + PH = AH Để C/m MP = NH ta cần C/m gì? Từ GT suy ra MP có tính chất gì? Ta cần C/m gì? Gọi I = MN AH thì ta có điều gì? Vì sao? Hoàn thành lời giải? Khi MH PN thì MH AB? Vì sao? AMH là tam giác gì? vì sao? ABH là tam giác gì? vì sao? Từ đó suy ra điều gì? Bài 3: Cho ABC. Gọi I là giao điểm của các tia phân giác trong. kẻ IM AB; IN BC và IK AC. Qua A vẽ đường thẳng a // MN; đường thẳng b // NK. A cắt NK tại E, b cắt NM tại D, ED lần lượt cắt AC, AB tại P, Q. Cmr: PQ // BC Gọi giao điểm của BC và AD là L, của BC và AE là H Để c/m: AM = AK ta c/m gì?, Tương tự hãy c/m: BN = BM, CN = CK MNHA là hình gì? Vì sao Ta suy ra điều gì? KNLA là hình gì? Vì sao? Từ đó ta có điều gì? Ta có thể KL gì về Mqh giữa ND, NE trong ALH DE có tính chất gì? Bài 4: Cho ABC có AB = c, BC = a, AC = b Qua A vẽ đường thẳng song song với BC cắt các tia phân giác của góc B và góc C tại D và E. Từ A vẽ AP BD; AQ CE. PQ lần lượt cắt BE, CD tại M và N Tính MN, PQ theo a, b, c Dự đoán xem MN có tính chất gì? Hãy C/m BCDE là hình thang Dự đoán và c/m dạng của BAD Từ đó ta có điều gì? PQ có tính chất gì? Suy ra tính chất của MN Hãy tính MN và PQ theo a, b, c HS ghi đề bài Viết GT, KL, vẽ hình HS suy nghĩ, tìm lời giải HS dự đoán c/m: MN // BC và Từ GT MN là đường trung bình của ABC MN // BC (1) và MN = BC (2) ABC đều nên (3) Từ (1) và (3) suy ra tứ giác BCNM là hình thang cân Chu vi hình thang cân BCNM là PBCNM = BC +BM + MN + NC (4) BM = NC = AB = BC = a BC = a, MN = BC = a Vậy : PBCNM = BC +BM + MN + NC = a + a + a + a = a Vẽ hình Tứ giác MPHN là hình thang cân hoặc C/m: MP và NH cùng bằng một đoạn nào đó MP là đường Tb của ABC nên MP // AC và MP = AC Ta cần C/m NH = AC M là trung điểm AB và MI // BH ( do MN là đường trung bình của ABC) nên I là trung điểm AH và AI MN (Do AH BC ) ANH cân tại N NH = NA = AC Vậy: MP = NH HS hoàn thành lời giải câu a Khi MH PN thì MH AB vì NP // AB AMH là tam giác vuông cân tại M vì có và có MI vừa là trung tuyến vừa là đường cao ABH có mà nên ABH vuông cân tại H. Suy ra BH = AH Mà BH = BP + PH = MN + PH Vậy: MN + PH = AH HS ghi đề, Vẽ hình, AMI = AKI (C. huyền – g. nhọn) AM = AK (1) BMI = BNI (C. huyền – g. nhọn) BM = BN (2) CNI = CKI (C. huyền – g. nhọn) CN = CK (3) MNHA là hình thang cân( vì có: MN//AH, ) NH = AM (4) KNLA là hình thang cân NL = AK (5) Từ (1), (4), (5) NL = NH (6) NE, ND là đường trung bình của ALH nên: EA = EH (7) và DA = DL (8) Từ (7) và (8) suy ra: DE là đường trung bình của ALH DE // LH PQ // BC HS vẽ hình Dự đoán: MN là đường trung bình của hình thang BCDE Từ gt BCDE là hình thang vì có DE // BC mà (so le trong – do BC // DE) BAD cân tại A. mà AP BD PB = PD; AB = AD = c Tương tự CAE cân tại A Và AQ CE QC = QE và AC = AE = b PQ là đoạn thẳng nối trung điểm của hai đường chéo hình thang BCDE nên PQ // AB MN là đường trung bình của hình thang BCDE nên: MN = = PQ = MN–(MQ + NP) = - BC = III. Bài tập về nhà: Bài 1: Cho hình thang vuông ABCD (AB // CD, = 900); AB = CD = AB kẻ CH AB, Gọi giao điểm của AC và DH là E, giao điểm của BD và CH là F Tứ giác ADCH là hình gì? b) C/m : AC BC c) EF = DC = AB Bài 2: Chứng minh rằng: Đoạn thẳng nối trung điểm hai đường chéo của hình thang thì song song với hai đáy và bằng nửa hiệu hai đáy II. Bài tập vận dụng: Hoạt động của GV Hoạt động của HS 1. Bài 1: Cho Hbh ABCD cú . Đường phõn giỏc của gúc D đi qua trung điểm của AB a) C/m: AB = 2AD b) Gọi F là trung điểm của CD. C/m ADF đều, AFC cõn c) C/m AC AD Giải Gọi E là trung điểm của AB. Ta cú ADE là tam giỏc gỡ? Vỡ sao? Hóy C/m điều đú Hóy C/m ADF cõn tại A cú một gúc 600 Hóy C/m AFC cõn tại F Từ AFC cõn tại F ta suy ra điều gỡ? Gúc DFA bằng hai lần gúc nào củaAFC =? 2. Bài 2: Cho ABC và O là điểm thuộc miền trong của tam giỏc đú. Gọi D, E, F lần lượt là trung điểm của AB, BC, CA và L, M, N lần lượt là trung điểm của OA, OB, OC Chứng minh rằng cỏc đoạn thẳng EL, FM, DN đồng quy Giải Để C/m ba đoạn thẳng EL, FM, DN đồng quy ta C/m gỡ? Ta C/m cỏc đoạn thẳng đú là đường chộo của hai hbh cú chung một đường chộo Để C/m tứ giỏc EFLM là Hbh ta c/m như thế nào? Tương tự ta cú tứ giỏc NLDE là hỡnh gỡ? Hai Hbh này cú chung đường chộo nào? Từ đú ta cú kết luận gỡ? Những Hbh nào cú tõm trựng nhau? 3. Bài 3: Cho hỡn chữ nhật ABCD; kẻ BHAC. Gọi E, F lần lượt là trung điểm của AH, CD. Chứng minh BE EF Giải Gọi K là trung điểm của AB ta cú điều gỡ? Vỡ sao? Tứ giỏc BCFK là hỡnh gỡ? Vỡ sao? EI cú tớnh chất gỡ? Vỡ sao? BFE là tam giỏc gỡ? Vỡa sao? 4. Bài 4: Cho ABC cõn tại A. Từ điểm D trờn BC kẻ đường vuụng gúc với BC cắt AB, AC lần lượt tại E, F. Dựng cỏc hỡnh chữ nhật BDEH và CDFK a) C/m: ba điểm A, H, K thẳng hàng b) C/m: A là trung điểm của HK c) Goi I, J theo thứ tự là tõm của cỏc hỡnh chữ nhật BDEH và CDFK. Tỡm tập hợp trung điểm M của đoạn thẳng IJ khi D di động trờn BC Để C/m A, H, K thẳng hàng ta c/m gỡ? Hóy C/m AH, AK cựng song song với một đường thẳng nào ? Hóy c/m tứ giỏc AIDJ là Hbh? Như thế nào? Từ I, J là tõm của cỏc hỡnh chữ nhật BDEH và CDFK và M là trung điểm của IJ ta suy ra điều gỡ? Từ MI // AH và MJ // AK ta suy ra điều gỡ Cú cỏch C/m nào khỏc? Ta đó cú A, H, K thẳng hàng nờn để c/m A là trung điểm của HK ta C/m gỡ? Hóy C/m AB // DK và kết hợp với I là trung điểm của DH để AH = AK Kẻ MN BC và đường cao AG thỡ MN cú tớnh chất gỡ? M cỏch BC một khoảng khụng đổi thỡ m nằm trờn đường nào? HS ghi đề, vẽ hỡnh a)ADE là tam giỏc cõn Ta cú , mà ABCD là Hbh nờn ADE cõn tại A AD = AE mà AB = 2 AE Nờn AB = 2AD b) AB = CD (do ABCD là Hbh) mà DF = CD, AD = AB. Suy ra AD = DF ADF cõn trại D cú vậy: ADF là tam giỏc đều Ta cú AF = DF (do ADF đều) Mà DF = FC (F là trung điểm của BC) Suy ra AF = FC AFC cõn tại F c) AFC cõn tại F (Gúc ngoài tại đỉnh của tam giỏc cõn) Mà (do ADF đều). Suy ra hay AC AD HS ghi đề, vẽ hỡnh HS suy nghĩ , phỏt biểu HS ghi nhớ phương phỏp c/m E, F là trung điểm của BC, CA EF là đường trung bỡnh của ABC suy ra EF // AB, EF = AB (1) Tương tự LM là đường trung bỡnh của OAB suy ra LM // AB, LM =AB (2) Từ (1) và (2) suy ra tứ giỏc EFLM là Hbh C/m tương tự ta cú tứ giỏc NLDE là Hbh (Vỡ cú NE //= LD) Hai Hbh EFLM và NLDE cú chung đường chộo LE hay ba đoạn thẳng EL, FM, DN đồng quy tại trung điểm của LE Hay ba Hbh EFLM , NFDM và NLDE cú tõm trựng nhau HS ghi đề, vẽ hỡnh Gọi K là trung điểm của AB ta cú EK // HB (Vỡ EK là đường trung bỡnh của AHB) mà BHAC EK AC suy ra CEK vuụng tại E Tứ giỏc BCFK cú BK //= CF và cú nờn là hỡnh chữ nhật nờn hai đường chộo BF và CK cắt nhau tại I và BF = CK I là trung điểm của BF , CK EI là trung tuyến thuộc cạnh huyền CK của CEK EI = CK = BF BFE cú trung tuyến EI = BF nờn là tam giỏc vuụng tại E BE EF HS ghi đề , vẽ hỡnh HS phỏt biểu C/m AH, AK cựng song song với IJ HS nờu cỏch c/m Từ I, J là tõm của cỏc hỡnh chữ nhật BDEH và CDFK và M là trung điểm của IJ ta suy ra MI và MJ lần lượt là đường trung bỡnh của cỏc tam giỏc AHD và AKD Nờn MI // AH và MJ // AK hay AH và AK cựng song song với IJ nờn A, H, K thẳng hàng (theo tiờn đề Ơclớt) HS nờu cỏch C/m khỏc ABC cõn tại A nờn (1) I là tõm của hcn BDEH nờn suy ra BID cõn tại I hay (2) Từ (1) và (2) suy ra AB // DK mà IH = ID nờn AH = AK mà A, H, K thẳng hàng nờn A là trung điểm của HK c) Kẻ MN BC (N BC); đường cao AG ta cú MN = AH (vỡ MN là đường trung bỡnh của ADG )khụng đổi, nờn M nằm trờn đường thẳng song song với BC và cỏch BC một khoảng bằng AH khụng đổi chớnh là đường trung bỡnh PQ của ABC (PQ // BC) III. Bài tập về nhà: Cho hỡnh chữ nhật ABCD. Kẻ BH vuụng gúc với AC. Gọi M, K theo thứ tự là trung điểm của AH và CD. Chứng minh BM vuụng gúc với MK cho hỡnh bỡnh hành ABCD. Vẽ ra phớa ngoài hỡnh bỡnh hành cỏc tam giỏc đều ABM, AND. Gọi E, F, Q theo thứ tự là trung điểm của BD, AN, AM a) tam giỏc MNC là tam giỏc gỡ? Vỡ sao? b) Tớnh Bài 1: Cho hỡnh thang cõn ABCD AB // CD, AB < CD. Gọi M, N, P , Q lần lượt là trung điểm của CD, AB, DB, CA a) C/m: NM là tia phõn giỏc của b) Tớnh số đo cỏc gúc của tứ giỏc MPNQ biết cỏc gúc nhọn của hỡnh thang ABCD là c) Hỡnh thang ABCD thoó món điều kiện gỡ thỡ tứ giỏc MPNQ là hỡnh vuụng? * Để C/m MN là tia phõn giỏc của Ta cần C/m gỡ? Để C/m MPNQ là hỡnh thoi ta C/m như thế nào? Hóy C/m MPNQ là Hỡnh bỡnh hành Bằng cỏch C/m cú hai cạnh đối vừa song song vừa bằng nhau, đú là hai cạnh nào? Hóy C/m NP //= MQ ? C/m MP = MQ để suy ra H.b.h MPNQ là hỡnh thoi MPNQ là hỡnh thoi ta suy ra điều gỡ ? bằng gúc nào? Vỡ sao? bằng gúc nào? Vỡ sao? =? = ? Hỡnh thoi MPNQ là hỡnh vuụng khi nào? Bài 2: Cho ABC vuụng cõn tại B. từ điểm D thuộc cạnh AB vẽ DE AC tại E, tia ED cắt tia CB tại F. Gọi M, N, P, Q lần lượt là trung điểm của AD, DF, FC, CA Chứng minh MNPQ là hỡnh vuụng Để C/m tứ giỏc MNPQ là hỡnh vuụng ta cần C/m điều gỡ? Để C/m tứ giỏc MNPQ là hỡnh chữ nhật ta cần C/m gỡ? Hóy C/m tứ giỏc MNPQ là hỡnh bỡnh hành? Để C/m H.b.h MNPQ là hỡnh chữ nhật thỡ ta C/m gỡ? Hóy C/m Hóy C/m H.b.h MNPQ là hỡnh thoi bằng cỏch C/m NP = MN Bài 3: Cho hỡnh vuụng ABCD, gọi I, K lần lượt là trung điểm của AD, DC; E là giao điểm của BI và AK a) chứng minh: BI AK b) Chứng minh CE = AB c) So sỏnh AK, BI, BK d) C/m: BD là phõn giỏc của * Để C/m BI AK ta C/m gỡ? Để C/m ta C/m bằng gúc nào? Vỡ sao? Hóy C/m AIB = DKA? Để C/m CE = AB ta C/m gỡ? AB =? Vậy để C/m CE = AB ta C/m CE = CB bằng cỏch C/m hai tam giỏc nào bằng nhau? Hay tam giỏc nào cõn? AK = BI? Vỡ sao? Ta cần C/m gỡ? (AK = BK hoặc BI = BK) hay khụng? Vỡ sao? HS ghi đề và vẽ hỡnh Ta C/m tứ giỏc MPNQ là hỡnh thoi C/m MPNQ là hỡnh bỡnh hành cú hai cạnh kề bằng nhau Từ GT NP là đường trung bỡnh của ADE nờn NP // AD và NP = AD (1) MQ là đường trung bỡnh của ADC nờn MQ // AD và MQ = AD (2) Từ (1) và (2) NP // MQ và NP = MQ suy ra tứ giỏc MPNQ là H.b.h Mặt khỏc MP = CB = AD (Vỡ AD = CB). Suy ra MP = MQ MPNQ là hỡnh thoi (H.b.h cú 2 cạnh kề bằng nhau) NM là tia phõn giỏc của b) MQ // AD (3) MP // CE (4) Từ (3) và (4) c) Hỡnh thoi MPNQ là hỡnh vuụng 0 Vậy: Hỡnh thang cõn ABCD cú 0 thỡ tứ giỏc MPNQ là hỡnh vuụng HS ghi đề bài và vẽ hỡnh Để C/m tứ giỏc MNPQ là hỡnh vuụng ta cần C/m MNPQ vừa là hỡnh chữ nhật vừa là hỡnh thoi MNPQ là hỡnh bỡnh hành cú một gúc vuụng Từ Gt MN là đường trung bỡnh của FCA MN // FA và MN = FA (1) Tương tự ta cú: PQ // FA và PQ = FA (2) Từ (1) và (2) suy ra MNPQ là H.b.h Mặt khỏc D là giao điểm của 2 đường cao AB và FE của FAC nờn CD là đường cao cũn lại của FAC CD FA PN FA PN MN (Vỡ MN // FA) Nờn tứ giỏc MNPQ là hỡnh chữ nhật (*) FCE vuụng tại E và cú (ABC vuụng cõn tại A) FCE vuụng cõn tại E DBF vuụng cõn tại B BD = BF nờn suy ra ABF = CBD FA = CD Mặt khỏc NP là đường trung bỡnh của FCD, nờn NP = CD = FA = MN hỡnh bỡnh hành MNPQ là hỡnh thoi (**) Từ (*) và (**) suy ra MNPQ là hỡnh vuụng HS ghi đề và vẽ hỡnh a) HS suy nghĩ, trả lời: C/m do ABI vuụng tại A Ta cần C/m AIB = DKA Vỡ cú AB = DA (ABCD là hỡnh vuụng) AI = DK (nửa cạnh hỡnh vuụng ABCD) AIB = DKA(c.g.c) mà ta cú BI AK b) Gọi F là trung điểm AB AKCF là H.b.h vỡ cú FA //= CK AK // CF CM BE hay CM là đường cao của của BCE (1) F là trung điểm AB mà MF // AK nờn M là trung điển BE hay CM là đường trung tuyến của BCE (2) Từ (1) và (2) suy ra BCE cõn tại B suy ra CE = CB mà CB = AB nờn CE = AB c) BI = AK (do AIB = DKA(c.g.c)- C/m ở cõu a) . IDB = KDB (c.g.c) vỡ cú: ID = KD (nửa cạnh hỡnh vuụng ABCD); (đường chộo DB là phõn giỏc của gúc D); DB chung BI = BK Vậy: AK = BI = BK d) IDB = KDB (c.g.c) nờn hay BD là tia phõn giỏc của III. Bài tập về nhà: Bài 1:Cho hỡnh vuụng ABCD . Từ điểm E trờn cạnh BC dựng , tia Ax cắt CD tại F. Gọi I là trung điểm FE, AI cắt CD tại M. Vẽ Ey // CD, Ey cắt AI tại K a) Tam giỏc AFE là tam giỏc gỡ? Vỡ sao? b) Tứ giỏc KFME là hỡnh gỡ? Vỡ sao? c) Chứng minh chu vi CEM khụng đổi khi E chuyển động trờn BC Bài 2: Cho ABCD là hỡnh vuụng. Gọi M, N, I, L lần lượt là trung điểm của AB, BC, CD, DA; DN lần lượt cắt AI, CM tại K và P; BL cắt AI, CM tại H và Q a) Chứng minh PA = DA b) Tứ giỏc KPQH là hỡnh gỡ? Vỡ sao?
Tài liệu đính kèm:
 bai_tap_on_boi_duong_hinh_hoc_lop_8_nam_hoc_2011_2012.doc
bai_tap_on_boi_duong_hinh_hoc_lop_8_nam_hoc_2011_2012.doc





