Bài kiểm tra môn Toán Lớp 8 - Học kỳ II - Năm học 2011-2012

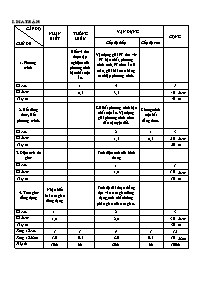
 I. Ma trËn:
CẤP ĐỘ
CHỦ ĐỀ
NHẬN BIẾT
THÔNG HIỂU
VẬN DỤNG
CỘNG
 Cấp độ thấp
Cấp độ cao
1. Phương trình
Hiểu và tìm được tập nghiệm của phương trình bậc nhất một ẩn.
Vận dụng giải PT đưa về:
PT bậc nhất, phương trình tích, PT chứa ẩn ở mẫu, giải bài toán bằng cách lập phương trình.
Số câu 
1
4
5 
Số điểm 
0,5
3,5
 4,0
điểm
 Tỉ lệ %
 40
%
2. Bất đẳng thức, Bất phương trình.
Giải bất phương trình bậc nhất một ẩn. Vận dụng giải phương trình chứa dấu trị tuyệt đối.
Chứng minh một bất đẳng thức.
Số câu 
2
1
3 
Số điểm 
1,5
0,5
 2,0
điểm
 Tỉ lệ %
 20
%
3. Diện tích đa giác
Tính diện tích của hình thang
Số câu 
1
1
Số điểm 
1,0
 1,0
điểm
 Tỉ lệ %
 10
%
4. Tam giác đồng dạng
Nhận biết hai tam giác đồng dạng 
Tính độ dài đoạn thẳng dựa vào tam giác đồng dạng, tính chất đường phân giác của tam giác.
Số câu 
1 
2
3
Số điểm 
1,0 
2,0
 3,0
điểm
 Tỉ lệ %
 30
%
Tổng số câu 
1
1
9
1
12
Tổng số điểm
1,0
0,5
8,0
0,5
10
điểm
Tỉ lệ %
10%
5%
80%
5%
100%
II. §Ò kiÓm tra:
Bài 1 (2,5 điểm): 
Giải các phương trình sau:
3x + 5 = 0 	
5x – 7 = 3(x - 1) + 6	
 (x + 1)(4x – 3) + 5(x + 1) = 0	
Bài 2 (1,5 điểm): 
Tìm x thỏa mãn:
4x – 5 > 2x + 2 
Bài 3 (1,5 điểm). Giải bài toán sau bằng cách lập phương trình:
 Một ôtô khởi hành từ A lúc 6 giờ sáng và dự định đến B lúc 10 giờ 30 phút cùng ngày. Do trời mưa, nên ôtô đã đi với vận tốc chậm hơn dự định 5km/h. Vì thế phải đến 11 giờ ôtô mới đến B. Tính quãng đường AB.
Bài 4 (1 điểm): Tính diện tích của một hình thang vuông, biết hai đáy có độ dài là 3cm và 6cm, góc tạo bởi một cạnh bên và đáy lớn có số đo bằng 45 độ.
Bài 5 (3 điểm): Cho tam giác vuông ABC vuông tại A với AC = 3cm, BC = 5cm. Vẽ đường cao AK.
Chứng minh rằng đồng dạng với và AB2 = BK.BC
Qua K kẻ KI // AB (I thuộc AC). Tính AK, KC, CI.
Phân giác góc BAC cắt BC tại D. Tính độ dài BD.
Bài 6 (0,5 điểm). Chứng minh bất đẳng thức: 
	a2 + b2 + c2 ab + bc + ac ; với mọi a, b, c thuộc R.
 III. h­íng dÉn chÊm vµ biÓu ®iÓm:
Bài
Nội dung
Điểm
1
(2,5 đ)
 3x + 5 = 0 	
ó 3x = - 5 
ó x = Vậy tập nghiệm của phương trình là S = { }
0,25
0,25
5x – 7 = 3(x - 1) + 6	
ó 5x – 7 = 3x – 3 + 6
ó 5x – 3x = - 3 + 6 + 7
ó 2x = 10
ó x = 5 Vậy tập nghiệm của phương trình là S = { 5 } 
0,25
0,25
(x + 1)(4x – 3) + 5(x + 1) = 0
ó (x + 1)(4x + 2) = 0
ó x + 1 = 0 hoặc 4x + 2 = 0
+) x + 1 = 0 ó x = - 1 +) 4x + 2 = 0 ó x = 	
 Vậy tập nghiệm của phương trình là S = { -1 ; }
0,25
0,25
0,25
ĐKXĐ: x ≠ -1 ; x ≠ 3
Qui đồng khử mẫu:
x(x + 1) + x(x – 3) = 9x
ó 2x2 – 11x = 0
ó x(2x – 11) = 0
ó x = 0 hoặc x = ; đều thỏa mãn ĐKXĐ
Vậy tập nghiệm của phương trình là S = { 0; }
0,25
0,25
0,25
2
(1,5 đ)
4x – 5 > 2x + 2 
ó 4x – 2x > 5 + 2
ó 2x > 7 
ó x > Vậy tập nghiệm của bpt là {x│x > }
0,25
0,25
+ Nếu 3x + 2 ≥ 0 ó x ≥ ; ta có PT:
 3x + 2 = 4x – 1 ó x = 3 (thỏa mãn)
+ Nếu 3x + 2 < 0 ó x < ; ta có PT:
 -3x - 2 = 4x - 1 ó x = (không thỏa mãn)
 Vậy tập nghiệm của phương trình là S = { 3 }
0,25
0,25
0,25
0,25
3
(1,5 đ)
Gọi quãng đường AB là x (km) ; ĐK: x > 0
Vận tốc theo dự định là: 
Vận tốc thực tế là: 
Vì vận tốc dự định nhanh hơn 5km/h nên ta có PT:
 - = 5 
Giải PT ta được: x = 225 (thoả mãn)
 Vậy quãng đường AB dài 225 km
0,25
0,25
0,25
0,25
0,25
0,25
4
(1,0 đ)
- Vẽ đúng hình:
A
B
C
D
H
- Gọi hình thang cần xét là ABCD vuông tại A và D.
- Kẻ BH và tính:
 BH = AB = DH = HC = 3cm
- Tính diện tích hình thang:
 (AB + CD).BH:2 = 13,5 (cm2)
0,25
0,5
0,25
5
(3,0 đ)
A
B
C
K
I
D
- Vẽ đúng hình:
0,25
a) đồng dạng với vì: vuông tại A và K; góc B chung
=> => AB2 = KB.BC (1)
0,5
0,5
b) Áp dụng định lý Py-ta-go vào tam giác ABC, ta có:
 AB2 = BC2 – AC2 = 25 – 9 = 16 => AB = 4 (cm)
- đồng dạng với 
 => => KA = (AB.AC):BC = (3.4):5 = 2,4 (cm)
- Từ (1) => KB = AB2 : BC = 16 : 5 = 3,2 (cm) 
 => CK = BC – KB = 5 – 3,2 = 1,8(cm)
- KI//AB, theo đl Ta-let ta có: 
 => CI = (AC.CK): BC =(3.1,8):5 = 1,08 (cm)
0,25
0,25
0,25
0,25
c) AD là phân giác của góc BAC nên ta có: 
=> BD = .AB = (cm)
0,5
0,25
6
(0,5đ)
 Ta có: a2 + b2 + c2 ab + bc + ac (1) ; với mọi a, b, c thuộc R
(1) ó 2(a2 + b2 + c2 ) 2(ab + bc + ac)
ó (a2 – 2ab + b2) + (a2 – 2ac + c2) + (b2 – 2bc + c2) 0
ó (a – b)2 + (a – c)2 + (b – c)2 0 luôn đúng (với mọi a, b, c thuộc R.) nên (1) luôn đúng.
0,25
0,25
Ghi chú: Học sinh làm theo cách khác đúng vẫn cho điểm tối đa.